某数学课外活动小组在学习了勾股定理之后,针对图1中所示的“由直角三角形三边向外侧作多边形,它们的面积 , , 之间的关系问题”进行了以下探究:
类比探究
(1)如图2,在 中, 为斜边,分别以 , , 为斜边向外侧作 , , ,若 ,则面积 , , 之间的关系式为 ;
推广验证
(2)如图3,在 中, 为斜边,分别以 , , 为边向外侧作任意 , , ,满足 , ,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;
拓展应用
(3)如图4,在五边形 中, , , , ,点 在 上, , ,求五边形 的面积.

在长方形纸片内部裁剪出一个长方形,尺寸如图所示.
(1)用含有a、b、x的代数式表示图中阴影部分的面积:;
(2)当 ,
, 时,求此时阴影部分的面积.
时,求此时阴影部分的面积.
已知:直线AB与直线CD相交于点O,∠BOC= ,
,

(1)如图1,若EO⊥AB,求∠DOE的度数;
(2)如图2,若EO平分∠AOC,求∠DOE的度数.
已知:关于x的方程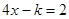 与
与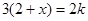 的解相同,求
的解相同,求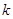 的值及相同的解.
的值及相同的解.
某校七年级举行踢毽比赛,参加的人数是未参加人数的3倍,如果该年级学生减少6人,未参加的学生增加6人,那么参加与未参加比赛的人数之比是2︰1,求该校七年级原有的人数.
已知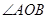 ,
,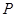 为
为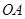 上一点.
上一点.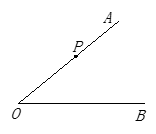
(1)过点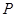 画一条直线
画一条直线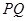 ,使
,使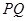 ∥
∥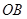 ;
;
(2)过点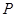 画一条直线
画一条直线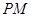 ,使
,使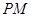 ⊥
⊥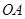 交
交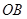 于点
于点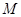 ;
;
(3)若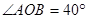 ,则
,则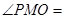 °.
°.