图①是某车站的一组智能通道闸机，当行人通过时智能闸机会自动识别行人身份，识别成功后，两侧的圆弧翼闸会收回到两侧闸机箱内，这时行人即可通过．图②是两圆弧翼展开时的截面图，扇形 和 是闸机的“圆弧翼”，两圆弧翼成轴对称， 和 均垂直于地面，扇形的圆心角 ，半径 ，点 与点 在同一水平线上，且它们之间的距离为 ．
（1）求闸机通道的宽度，即 与 之间的距离（参考数据： ， ， ；
（2）经实践调查，一个智能闸机的平均检票速度是一个人工检票口平均检票速度的2倍，180人的团队通过一个智能闸机口比通过一个人工检票口可节约3分钟，求一个智能闸机平均每分钟检票通过的人数．
（·湖南长沙）若关于x的二次函数y=a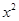
+bx+c（a＞0，c＞0，a、b、c是常数）与x轴交于两个不同的点A（
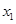，0），B（
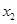，0）（0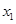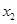＜＜），与y轴交于点P，其图像顶点为点M，点O为坐标原点。
（1）当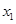=c=2，a=
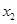时，求与b的值；
（2）当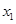=2c时，试问△ABM能否为等边三角形？判断并证明你的结论；
（3）当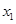=mc（m＞0）时，记△MAB，△PAB的面积分别为S1，S2，若△BPO∽△PAO，且S1=S2,求m的值。
|
（·湖南长沙）如图，在直角坐标系中，⊙M经过原点O（0,0），点A（
，0）与点B（0，－
），点D在劣弧OA上，连接BD交x轴于点C，且∠COD=∠CBO。
（1）求⊙M的半径；
（2）求证：BD平分∠ABO；
（3）在线段BD的延长线上找一点E，使得直线AE恰为⊙M的切线，求此时点E的坐标。
（·湖南常德）如图，在菱形ABCD中，E是CD上的一点，连接BE交AC于O，连接DO并延长交BC于E。
（1）求证：△FOC≌△EOC
（2）将此图中的AD、BE分别延长交于点N，作EM∥BC交CN于M，再连接FM即得到图5。
求证：①
；②FD＝FM
（·湖北武汉，22题，分）（本题8分）已知锐角△ABC中，边BC长为12，高AD长为8
（1） 如图，矩形EFGH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K
① 求
的值
② 设EH=x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值
（2） 若ABAC，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC的另两边上，直接写出正方形PQMN的边长．
（·湖北黄冈，24题，分）（14 分）如图，在矩形OABC 中，OA=5，AB=4，点D 为边AB 上一点，将△BCD 沿直线CD 折叠，使点B 恰好落在OA边上的点E 处，分别以OC，OA 所在的直线为x 轴，y 轴建立平面直角坐标系．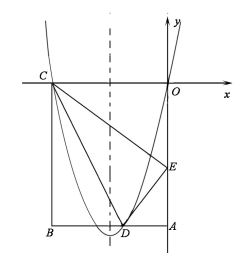
（1）求OE 的长；
（2）求经过O，D，C 三点的抛物线的解析式；
（3）一动点P 从点C 出发，沿CB 以每秒2 个单位长的速度向点B 运动，同时动点Q 从E 点出发，沿EC 以每秒1 个单位长的速度向点C 运动，当点P 到达点B 时，两点同时停止运动．设运动时间为t 秒，当t为何值时，DP=DQ；
（4） 若点N 在（2）中的抛物线的对称轴上，点M 在抛物线上，是否存在这样的点M与点N，使得以M，N，C，E 为顶点的四边形是平行四边形？若存在，请求出M 点的坐标；若不存在，请说明理由．