为了解学生掌握垃圾分类知识的情况，增强学生环保意识．某学校举行了“垃圾分类人人有责”的知识测试活动，现从该校七、八年级中各随机抽取20名学生的测试成绩（满分10分，6分及6分以上为合格）进行整理、描述和分析，下面给出了部分信息．
七年级20名学生的测试成绩为：7，8，7，9，7，6，5，9，10，9，8，5，8，7，6，7，9，7，10，6．
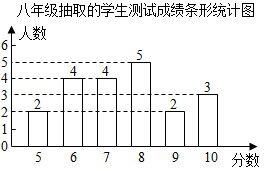
八年级20名学生的测试成绩条形统计图如图：
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、8分及以上人数所占百分比如下表所示：
年级 |
平均数 |
众数 |
中位数 |
8分及以上人数所占百分比 |
七年级 |
7.5 |
|
7 |
|
八年级 |
7.5 |
8 |
|
|
根据以上信息，解答下列问题：
（1）直接写出上述表中的 ， ， 的值；
（2）根据上述数据，你认为该校七、八年级中哪个年级学生掌握垃极分类知识较好？请说明理由（写出一条理由即可）；
（3）该校七、八年级共1200名学生参加了此次测试活动，估计参加此次测试活动成绩合格的学生人数是多少？
如图，已知二次函数
的图象的对称轴为直线
，且与
轴有两个不同的交点，其中一个交点坐标为
．
（1）求二次函数的关系式；
（2）在抛物线上有一点
，其横坐标为-2，直线
过点
并绕着点
旋转，与抛物线的另一个交点是点
，点
的横坐标满足
，当
的面积最大时，求出此时直线
的关系式；
（3）抛物线上是否存在点
使
的面积与（2）中
的最大面积相等．若存在，求出点
的横坐标；若不存在说明理由．
如图（Ⅰ），在平面直角坐标系中，⊙O′是以点O′（2，﹣2）为圆心，半径为2的圆，⊙O″是以点O″（0，4）为圆心，半径为2的圆．
（1）将⊙O′竖直向上平移2个单位，得到⊙O1，将⊙O″水平向左平移1个单位，得到⊙O2如图（Ⅱ），分别求出⊙O1和⊙O2的圆心坐标．
（2）两圆平移后，⊙O2与y轴交于A、B两点，过A、B两点分别作⊙O2的切线，交x轴与C、D两点，求△O2AC和△O2BD的面积
．
某经营世界著名品牌的总公司，在我市有甲、乙两家分公司，这两家公司都销售香水和护肤品．总公司现香水70瓶，护肤品30瓶，分配给甲、乙两家
分公司，其中40瓶给甲公司，60瓶给乙公司，且都能卖完，两公司的利润（元）如下表．
（1）假设总公司分配给甲公司x瓶香水，求：甲、乙两家公司的总利润W与x之间的函数关系式；
（2）在（1）的条件下，甲公司的利润会不会比乙公司的利润高？并说明理由；
（3）若总公司要求总利润不低于17370元，请问有多少种不同的分配
方案，并将各种方案设计出来．
| 每瓶香水利润 |
每瓶护肤品利润 |
|
| 甲公司 |
180 |
200 |
| 乙公司 |
160 |
150 |
一个不透明的袋子中，装有红黑两种颜色的小球（除颜色不同外其他都相同），其中一个红球，两个分别标有A、B黑球．
（1）小李第一次从口袋中摸出一个球，并且不放回，第二次又从口袋中摸出一个球，则小李两次都摸出黑球的概率是多少？试用树状图或列表法加以说明；
（2）小张第一次从口袋中摸出一个球，摸到红球不放回，摸到黑球放回．第二次又从口袋中摸出一个球，则小张第二次摸到黑球的概率是多少？试用
树状图或列表法加以说明．
如图，已知反比例函数
（m是常数，m≠0），一次函数y=ax+b（a、b为常数，a≠0），其中一次函数与x轴，y轴的交点分别是A（﹣4，0），B（0，2）．
（1）求一次函数的关系式；
（2）反比例函数图象上有一点P满足：①PA⊥x轴；②PO=
（O为坐标原点），求反比例函数的关系式；
（3）求点P关于原点的对称点Q的坐标，判断点Q是否在该反比例函数的图象上．