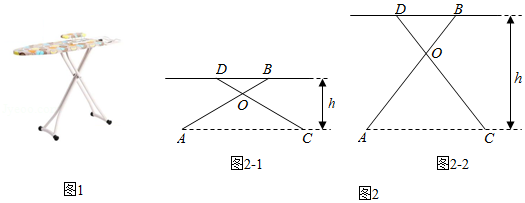
有一种升降熨烫台如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度．图2是这种升降熨烫台的平面示意图． 和 是两根相同长度的活动支撑杆，点 是它们的连接点， ， 表示熨烫台的高度．
（1）如图 ．若 ， ，求 的值；
（2）爱动脑筋的小明发现，当家里这种升降熨烫台的高度为 时，两根支撑杆的夹角 是 （如图 ．求该熨烫台支撑杆 的长度（结果精确到 ．
（参考数据： ， ， ，
a，b为两个有理数，表示在数轴上的位置如图所示，把-a，-b在数轴上表示出来，再把a，b，-a，-b，0按从小到大的顺序排列出来。
一辆货车从超市出发，向东走了2km，到达小刚家，继续向东走了3km到达小红家，又向西走了9km到达小英家，最后回到超市.
⑴请以超市为原点，以向东方向为正方向，用1个单位长度表示1km，画出数轴。并在数轴上表示出小刚家、小红家、小英家的位置；
⑵小英家距小刚家有多远？
⑶货车一共行驶了多少千米？
计算：（1）
（2）33.1－10.7－（－22.9）－
（3）
（4）
（5）
（6）
把下列各数填入大括号：-2.4，3，2.004，-
，1
， -
，0，π，-(-2.28)，3.14，-|-4|， -2.1010010001…（每两个1之间依次增加1个0）
正有理数集合：（…）整数集合：（…）
负分数集合：（…）无理数集合：（…）
如图，△ABC中，∠ACB=90°，AC=BC，将△ABC绕点C逆时针旋转角α．（0°＜α＜90°）得到△
，连接．设
交AB于D，
分别交AB、AC于E、F．
（1）在图中不再添加其它任何线段的情况下，请你找出一对全等的三角形，并加以说明（△ABC与△全等除外）；
（2）当△
是等腰三角形时，求α；