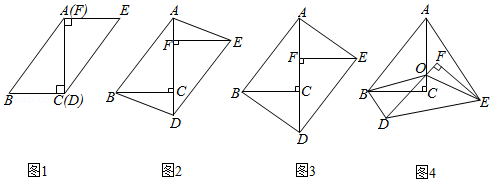
在一次数学研究性学习中,小兵将两个全等的直角三角形纸片 和 拼在一起,使点 与点 重合,点 与点 重合(如图 ,其中 , , ,并进行如下研究活动.
活动一:将图1中的纸片 沿 方向平移,连结 , (如图 ,当点 与点 重合时停止平移.
[思考]图2中的四边形 是平行四边形吗?请说明理由.
[发现]当纸片 平移到某一位置时,小兵发现四边形 为矩形(如图 .求 的长.
活动二:在图3中,取 的中点 ,再将纸片 绕点 顺时针方向旋转 度 ,连结 , (如图 .
[探究]当 平分 时,探究 与 的数量关系,并说明理由.
为了解南京市2012年市城镇非私营单位员工每月的收入状况,统计局对市城镇非私营单位随机抽取了1000人进行抽样调查.整理样本数据,得到下列图表:
市城镇非私营单位1000人月收入频数分布表
(1)如果1000人全部在金融行业抽取,这样的抽样是否合理?请说明理由;
(2)根据这样的调查结果,绘制条形统计图;
(3)2012年南京市城镇非私营单位月平均工资为5034元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理?
甲、乙、丙三位歌手进入“我是歌手”的冠、亚、季军的决赛,他们通过抽签来决定演唱顺序.
(1)求甲第一位出场的概率;
(2)求甲比乙先出场的概率.
已知:如图,在正方形ABCD中,点E、F在对角线BD上,且BF=DE.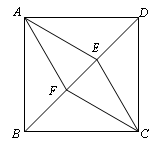
(1)求证:四边形AECF是菱形.
(2)若AB=2,BF=1,求四边形AECF的面积.
解不等式组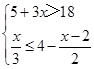 ,并写出不等式组的整数解.
,并写出不等式组的整数解.
(本小题满分11分)
如图,在平面直角坐标系中,已知点A(0,2),点P是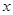 轴上一动点,以线段AP为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q的位置为B.
轴上一动点,以线段AP为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q的位置为B.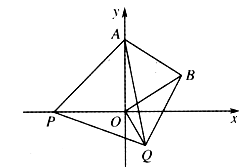
(1)求点B的坐标;
(2)求证:当点P在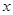 轴上运动(P不与O重合)时,∠ABQ为定值;
轴上运动(P不与O重合)时,∠ABQ为定值;
(3)是否存在点P,使得以A,O,Q,B为顶点的四边形是梯形?若存在,请求出P点的坐标;若不存在,请说明理由.