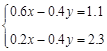如图,抛物线 与 轴相交于 , 两点,与 轴相交于点 , , ,直线 是抛物线的对称轴,在直线 右侧的抛物线上有一动点 ,连接 , , , .
(1)求抛物线的函数表达式;
(2)若点 在 轴的下方,当 的面积是 时,求 的面积;
(3)在(2)的条件下,点 是 轴上一点,点 是抛物线上一动点,是否存在点 ,使得以点 , , , 为顶点,以 为一边的四边形是平行四边形,若存在,求出点 的坐标;若不存在,请说明理由.

如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.
(1)在平面直角坐标系中画出探险路线图;
(2)分别写出A、B、C、D、P点的坐标.
小明想了解全校3000名同学对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从中抽取一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图(如图甲,图乙)
(1)求出图乙中a,b的值,并补全条形图;
(2)若此次调查中喜欢体育节目的女同学有10人,请估算该校喜欢体育节目的女同学有多少人?

图甲图乙
如图,点E在直线DF上,点B在直线AC上,DB、EC分别交AF于点G、H,若∠AGB=∠EHF,∠C=∠D,请你判断∠A和∠F的大小关系,并说明你的理由.
解不等式组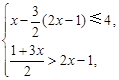 把解集表示在数轴上,并写出不等式组的整数解.
把解集表示在数轴上,并写出不等式组的整数解.
解方程组