今年疫情期间,针对各种入口处人工测量体温存在的感染风险高、效率低等问题,清华大学牵头研制一款“测温机器人”,如图1,机器人工作时,行人抬手在测温头处测量手腕温度,体温合格则机器人抬起臂杆行人可通行,不合格时机器人不抬臂杆并报警,从而有效阻隔病原体.

(1)为了设计“测温机器人”的高度,科研团队采集了大量数据.下表是抽样采集某一地区居民的身高数据:
测量对象 |
男性 岁) |
女性 岁) |
|||||
抽样人数(人 |
2000 |
5000 |
20000 |
2000 |
5000 |
20000 |
|
平均身高(厘米) |
173 |
175 |
176 |
164 |
165 |
164 |
|
根据你所学的知识,若要更准确的表示这一地区男、女的平均身高,男性应采用 176 厘米,女性应采用 厘米;
(2)如图2,一般的,人抬手的高度与身高之比为黄金比时给人的感觉最舒适,由此利用(1)中的数据得出测温头点 距地面105厘米.指示牌挂在两臂杆 , 的连接点 处, 点距地面110厘米.臂杆落下时两端点 , 在同一水平线上, 厘米,点 在点 的正下方5厘米处.若两臂杆长度相等,求两臂杆的夹角.
(参考数据表)
计算器按键顺序 |
计算结果(近似值) |
计算器按键顺序 |
计算结果(近似值) |
|
0.1 |
|
78.7 |
|
0.2 |
|
84.3 |
|
1.7 |
|
5.7 |
|
3.5 |
|
11.3 |
如图,有一长方形的仓库,一边长为5米.现要将它改建为简易住房,改建后的住房分为客厅、卧室和卫生间三部分,其中客厅和卧室都为正方形,且卧室的面积大于卫生间的面积.若改建后卫生间的面积为6平方米,试求长方形仓库另一边的长.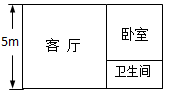
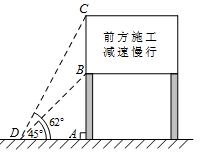
进入3月份,我市“两横三纵”快速路系统全线开工.为缓解市区内一些主要路段交通拥挤的现状,交警部门在一些主要路口设立了如图所示的交通路况显示牌.已知立杆AB的高度是3米,从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°.求路况显示牌BC的高度.(精确到0.1米)
【参考数据: ,
,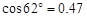 ,
,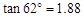 】
】
电动自动车已成为市民日常出行的首选工具.据某市某品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月份销售216辆.
(1)求该品牌电动自行车销售量的月均增长率;
(2)若该品牌电动自行车的进价为2300元,售价为2800元,则该经销商1至3月共盈利多少元?
如图,在平面直角坐标系中,△AOB的顶点坐标分别为A(2,1)、O(0,0)、B(1,-2).
(1)P(a,b)是△AOB的边AB上一点,△AOB经平移后点P的对应点为P2(a-3, b+1),请画出上述平移后的△A1O1B1,并写出点A1的坐标;
(2)以点O为位似中心,在y轴的右侧画出△AOB的一个位似△A2OB2,使它与△AOB的相似比为2:1,并分别写出点A、P的对应点A2、P2的坐标;
(3)判断△A2OB2与△A1O1B1能否是关于某一点Q为位似中心的位似图形,若是,请在图10中标出位似中心Q,并写出点Q的坐标.
如图,矩形ABCD中,E为BC上一点,DF⊥AE于点F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,AD=12,BE=8,求DF的长.