古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的圆”，请研究如下美丽的圆，如图， 中， ， ， ，点O在线段 上，且 ，以O为圆心． 为半径的 交线段AO于点D，交线段AO的延长线于点E．
（1）求证： 是 的切线；
（2）研究过短中，小明同学发现 ，回答小明同学发现的结论是否正确？如果正确，给出证明；如果不正确，说明理由．
如图，路灯（
点）距地面8米，身高1.6米的小明从距路灯的底部（
点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？
如图，一次函数
的图象与反比例函数
的图象交于点P，点P在第一象限．PA⊥x轴于点A，PB⊥y轴于点B．一次函数的图象分别交
轴、
轴于点C、D，且S△PBD＝4，
．
求点D的坐标；
求一次函数与反比例函数的解析式；
根据图象写出当
时，一次函数的值大于反比例
函数的值的的取值范围.
如图D，E分别是△ABC的AB，AC边上的点，且DE∥BC，AD∶AB=1∶4，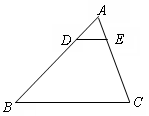
证明：△ADE∽△ABC
当DE=2，求BC的长.
已知∠AOB=90°，OM是∠AOB的平分线，将三角板的直角顶点P放在射线OM上滑动，两直角边分别与OA、OB交于C、D，PC和PD有怎样的数量关系，证明你的结论。
先阅读下面材料，再解答所提出的问题
老师在给同学们作已知角的平分线：
已知:∠AOB.
求作：射线OC，使∠AOC=∠BOC.