在数的学习过程中,我们总会对其中一些具有某种特性的数充满好奇,如学习自然数时,我们发现一种特殊的自然数﹣﹣“好数”.
定义:对于三位自然数n,各位数字都不为0,且百位数字与十位数字之和恰好能被个位数字整除,则称这个自然数n为“好数”.
例如: 是“好数”,因为4,2,6都不为0,且 ,6能被6整除;
643不是“好数”,因为 ,10不能被3整除.
(1)判断 , 是否是“好数”?并说明理由;
(2)求出百位数字比十位数字大5的所有“好数”的个数,并说明理由.
学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12.
请你回答:
(1)本次活动共有件作品参赛;各组作品件数的众数是件;
(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?
(3)小制作评比结束后,组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示作品B、D的概率.
如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.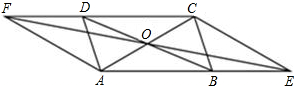
(1)计算:
(2)化简:
设抛物线y=mx2-3mx+2(m≠0)与x轴的交点为A(x1,0),B(x2,0),且x12+x22=17,其中x1<x2,点P(a,b)为抛物线上一动点.
(1)求抛物线的解析式;
(2)连接AC,过P点做直线PE∥AC交x轴于点E,交y轴于点F(O,t),当a取何值时t有最大值,最大值是多少?
(3)判断在(2)的条件中是否存在一点P,使以点A、C、P、E为顶点的四边形为平行四边形.若不存在试说明理由;若存在,试求出点P的坐标.
阅读材料:
关于三角函数还有如下的公式:
sin(α±β)="sinαcosβ±cosαsinβ"
tan(α±β)= .
.
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:tan15°=tan(45°-30°)=
=
根据以上阅读材料,请选择适当的公式解答下面问题
(1)计算:sin15°;
(2)乌蒙铁塔是六盘水市标志性建筑物之一(图1),小华想用所学知识来测量该铁塔的高度,如图2,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出乌蒙铁塔的高度.(精确到0.1米,参考数据 =1.732,
=1.732, =1.414)
=1.414)