某商场为了吸引顾客，设计了一个摸球获奖的箱子，箱子中共有20个球，其中红球2个，兰球3个，黄球5个，白球10个，并规定购买100元的商品，就有一次摸球的机会，摸到红、兰、黄、白球的(一次只能摸一个)，顾客就可以分别得到80元、30元、10元、0元购物卷，凭购物卷仍然可以在商场购买，如果顾客不愿意摸球，那么可以直接获得购物卷10元.
(1)每摸一次球所获购物卷金额的平均值是多少？
(2)你若在此商场购买100元的货物，两种方式中你应选择哪种方式？为什么？
（本题6分）如图，四边形ABCD中，AB=3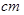
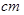，AD=4，BC=13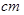，CD=12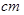，∠A=90°，求BD的长和四边形ABCD的面积．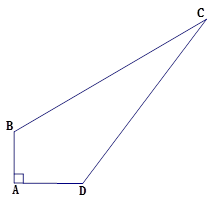 
（本题6分）已知△ABC中，AB=AC=5，BC=6， AM平分∠BAC, D为AC的中点，E为BC延长线上一点，且CE=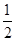
BC．（1）求ME的长;（2）求证：DB=DE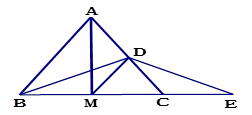
（本题5分）电信局要修建一座电信发射塔，如图，按照设计要求，发射塔到两个城镇A、B的距离必须相等，到两条高速公路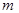
和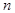
的距离也必须相等，发射塔应修建在什么位置？请用直尺和圆规作出该位置并在图上标出．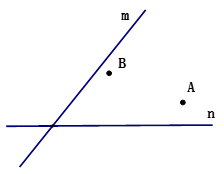 
（本题6分）如图，△ABC≌△DEF，∠A=30°，∠B=50°，BF=2，求∠DFE的度数与EC的长．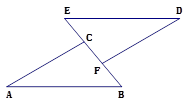 
（本题12分）如图，△ABC和△CDE均为等腰三角形，AC=BC，CD=CE，AC>CD，∠ACB=∠DCE且点A、D、E在同一直线上，连接BE．
（1）若∠ACB="60°," 则∠AEB的度数为；
线段AD、BE之间的数量关系是．
（2）若∠ACB=∠DCE="90°," CM为△DCE中DE边上的高．
①求∠AEB的度数．
②若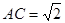
，
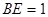，试求CM的长．（请写全必要的证明和计算过程）