如图所示,电阻为 的正方形单匝线圈 的边长为 , 边与匀强磁场边缘重合。磁场的宽度等于线圈的边长,磁感应强度大小为 .在水平拉力作用下,线圈以 的速度向右穿过磁场区域。求线圈在上述过程中
(1)感应电动势的大小 ;
(2)所受拉力的大小 ;
(3)感应电流产生的热量 。

(1)一列简谐横波沿x轴正方向传播,在t=0和t=0.20 s时的波形分别如图中实线和虚线所示。己知该波的周期T>0.20 s。下列说法正确的是( )
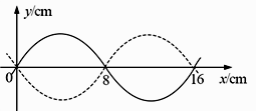
A.波速为0.40 m/s
B.波长为0.08 m
C. x=0.08 m的质点在 t=0.70 s时位于波谷
D. x=0.08 m的质点在 t=0.12 s时位于波谷
E.若此波传入另一介质中其波速变为0.80 m/s,则它在该介质中的波长为0.32 m
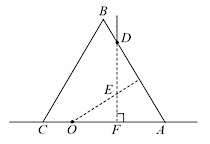
(2)如图,某同学在一张水平放置的白纸上画了一个小标记"·"(图中 O点),然后用横截面为等边三角形 ABC的三棱镜压在这个标记上,小标记位于 AC边上。 D位于 AB边上,过 D点做 AC边的垂线交 AC于 F。该同学在 D点正上方向下顺着直线 DF的方向观察。恰好可以看到小标记的像;过 O点做 AB边的垂线交直线 DF于 E; DE=2 cm, EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
如图,在竖直平面内,一半径为R的光滑圆弧轨道ABC和水平轨道PA在A点相切。BC为圆弧轨道的直径。O为圆心,OA和OB之间的夹角为α,sinα=
,一质量为m的小球沿水平轨道向右运动,经A点沿圆弧轨道通过C点,落至水平轨道;在整个过程中,除受到重力及轨道作用力外,小球还一直受到一水平恒力的作用,已知小球在C点所受合力的方向指向圆心,且此时小球对轨道的压力恰好为零。重力加速度大小为g。求:

(1)水平恒力的大小和小球到达 C点时速度的大小;
(2)小球到达 A点时动量的大小;
(3)小球从 C点落至水平轨道所用的时间。
如图,从离子源产生的甲、乙两种离子,由静止经加速电压U加速后在纸面内水平向右运动,自M点垂直于磁场边界射入匀强磁场,磁场方向垂直于纸面向里,磁场左边界竖直。已知甲种离子射入磁场的速度大小为v 1, 并在磁场边界的N点射出;乙种离子在MN的中点射出;MN长为l。不计重力影响和离子间的相互作用。求:

(1)磁场的磁感应强度大小;
(2)甲、乙两种离子的比荷之比。
(1)如图,一定质量的理型气体从状态a开始,经历过程①、②。③、④到达状态e,对此气体,下列说法正确的是( )

| A. |
过程①中气体的压强逐渐减小 |
| B. |
过程②中气体对外界做正功 |
| C. |
过程④中气体从外界吸收了热量 |
| D. |
状态c、d的内能相等 |
| E. |
状态d的压强比状态b的压强小 |
(2)如图,容积为V的汽缸由导热材料制成,面积为S的活塞将汽缸分成容积相等的上下两部分,汽缸上部通过细管与装有某种液体的容器相连,细管上有一阀门K。开始时,K关闭,汽缸内上下两部分气体的压强均为P 0,现将K打开,容器内的液体缓慢地流入汽缸,当流入的液体体积为 时,将K关闭,活塞平衡时其下方气体的体积减小了 ·,不计活塞的质量和体积,外界温度保持不变,重力加速度大小为g。求流入汽缸内液体的质量。

一质量为m的烟花弹获得动能E后,从地面竖直升空,当烟花弹上升的速度为零时,弹中火药爆炸将烟花弹炸为质量相等的两部分,两部分获得的动能之和也为E,且均沿竖直方向运动。爆炸时间极短,重力加速度大小为g,不计空气阻力和火药的质量,求
(1)烟花弹从地面开始上升到弹中火药爆炸所经过的时间.
(2)爆炸后烟花弹向上运动的部分距地面的最大高度.