已知抛物线 与 轴只有一个公共点.
(1)若抛物线过点 ,求 的最小值;
(2)已知点 , , 中恰有两点在抛物线上.
①求抛物线的解析式;
②设直线 与抛物线交于 , 两点,点 在直线 上,且 ,过点 且与 轴垂直的直线分别交抛物线和 于点 , .求证: 与 的面积相等.
为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点 处测得河北岸的树 恰好在 的正北方向.测量方案与数据如下表:
|
课题 |
测量河流宽度 |
||
|
测量工具 |
测量角度的仪器,皮尺等 |
||
|
测量小组 |
第一小组 |
第二小组 |
第三小组 |
|
测量方案示意图 |
|
|
|
|
说明 |
点 , 在点 的正东方向 |
点 , 在点 的正东方向 |
点 在点 的正东方向,点 在点 的正西方向. |
|
测量数据 |
, , . |
, , . |
, , . |
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个方案及其数据求出河宽(精确到 .(参考数据: , , ,

小吴家准备购买一台电视机,小吴将收集到的某地区 、 、 三种品牌电视机销售情况的有关数据统计如下:
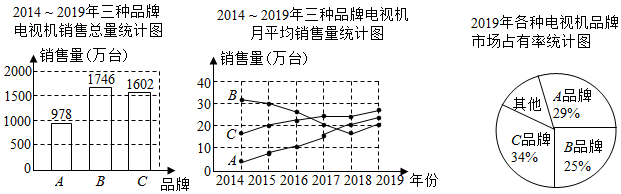
根据上述三个统计图,请答案:
(1) 年三种品牌电视机销售总量最多的是 品牌,月平均销售量最稳定的是 品牌.
(2)2019年其他品牌的电视机年销售总量是多少万台?
(3)货比三家后,你建议小吴家购买哪种品牌的电视机?说说你的理由.
经过实验获得两个变量 , 的一组对应值如下表.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
6 |
2.9 |
2 |
1.5 |
1.2 |
1 |
(1)请画出相应函数的图象,并求出函数表达式.
(2)点 , , , 在此函数图象上.若 ,则 , 有怎样的大小关系?请说明理由.

已知:如图,在 中, , 与 相切于点 .求证: .小明同学的证明过程如下框:
|
证明:连结 , , , 又 , , . |
小明的证法是否正确?若正确,请在框内打“ ”;若错误,请写出你的证明过程.

比较 与 的大小.
(1)尝试(用“ ”,“ ”或“ ”填空)
①当 时, ;
②当 时, ;
③当 时, .
(2)归纳:若 取任意实数, 与 有怎样的大小关系?试说明理由.