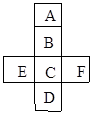为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点 处测得河北岸的树 恰好在 的正北方向.测量方案与数据如下表:
课题 |
测量河流宽度 |
||
测量工具 |
测量角度的仪器,皮尺等 |
||
测量小组 |
第一小组 |
第二小组 |
第三小组 |
测量方案示意图 |
|
|
|
说明 |
点 , 在点 的正东方向 |
点 , 在点 的正东方向 |
点 在点 的正东方向,点 在点 的正西方向. |
测量数据 |
, , . |
, , . |
, , . |
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个方案及其数据求出河宽(精确到 .(参考数据: , , ,

解方程:
若 ,求
,求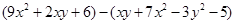 的值.
的值.
先化简,再求值: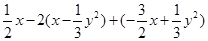 ,其中
,其中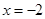 ,
,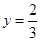 .
.
在密码学中,你直接可以看到的内容为明文(真实文),对明文进行某种处理后得到的内容为密文.现有一种密码把英文的明文单词按字母分解,其中英文的26个字母(不论大小写)依次对应1,2,3,……26这26个自然数,见以下表格:
| a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
| 14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
现给出一个公式: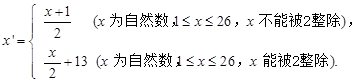
将明文字母对应的数字x按以上公式计算得到密文字母对应的数字x',比如明文字母为g,g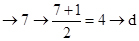 ,所以明文字母g对应的密文字母为d.
,所以明文字母g对应的密文字母为d.
按照上述规定,将明文good译成的密文是什么?写出你的计算过程;
正方体六个面展开如图所示,六个面分别用字母A、B、C、D、E、F表示,已知: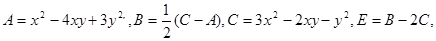 若正方体相对的两个面上的多项式的和相等,求D、F. (用含
若正方体相对的两个面上的多项式的和相等,求D、F. (用含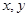 的多项式表示)
的多项式表示)