已知在 中， 为 边的中点，连接 ，将 绕点 顺时针方向旋转（旋转角为钝角），得到 ，连接 ， ．
（1）如图1，当 且 时，则 与 满足的数量关系是 ；
（2）如图2，当 且 时，（1）中的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由．
（3）如图3，延长 到点 ，使 ，连接 ，当 ， 时，求 的长．
画△ABC，使其两边为已知线段a、b，夹角为β．（要求：用尺规作图，写出已知、求作；保留作图痕迹；不在已知的线、角上作图；不写作法）．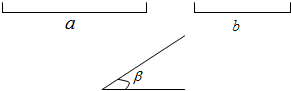
已知：
求作：
解分式方程：
．
（本小题8分）随着人们节能环保意识的增强，绿色交通工具越来越受到人们的青睐，电动摩托成为人们首选的交通工具，某商场计划用不超过
元购进
、
两种不同品牌的电动摩托
辆，预计这批电动摩托全部销售后可获得不少于
元的利润，、两种品牌电动摩托的进价和售价如下表所示：
设该商场计划进品牌电动摩托
辆，两种品牌电动摩托全部销售后可获利润
元.
写出与之间的函数关系式；
该商场购进品牌电动摩托多少辆时？获利最大，最大利润是多少？
（本小题8分）为贯彻落实云南省教育厅提出的“三生教育”，在母亲节来临之际，某校团委组织了以“珍爱生命，学会生存，感恩父母”为主题的教育活动，在学校随机调查了
名同学平均每周在家做家务的时间，统计并制作了如下的频数分布和扇形统计图：
根据上述信息回答下列问题：
，
；
在扇形统计图中，
组所占圆心角的度数为；
全校共有
名学生，估计该校平均每周做家务时间不少于
小时的学生约有多少人？
（本小题8分）先化简
，再从
、
、
三个数中，选择一个你认为合适的数作为
的值代入求值.