已知抛物线: 与 轴交点为 , 在 的左侧),顶点为 .
(1)求点 , 的坐标及抛物线的对称轴;
(2)若直线 与抛物线交于点 , ,且 , 关于原点对称,求抛物线的解析式;
(3)如图,将(2)中的抛物线向上平移,使得新的抛物线的顶点 在直线 上,设直线 与 轴的交点为 ,原抛物线上的点 平移后的对应点为点 ,若 ,求点 , 的坐标.

解不等式组: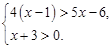
定义符号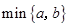 的含义为:当
的含义为:当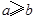 时,
时, 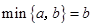 ;当
;当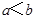 时,
时, 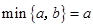 .如:
.如: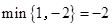 ,
,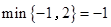 .
.
(1)求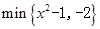 ;
;
(2)已知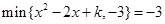 , 求实数
, 求实数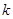 的取值范围;
的取值范围;
(3) 已知当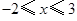 时,
时,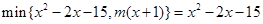 .直接写出实数
.直接写出实数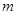 的取值范围.
的取值范围.
已知:Rt△A′BC′和 Rt△ABC重合,∠A′C′B=∠ACB=90°,∠BA′C′=∠BAC=30°,现将Rt△A′BC′ 绕点B按逆时针方向旋转角α(60°≤α≤90°),设旋转过程中射线C′C和线段AA′相交于点D,连接BD.
(1)当α=60°时,A’B 过点C,如图1所示,判断BD和A′A之间的位置关系,不必证明;
(2)当α=90°时,在图2中依题意补全图形,并猜想(1)中的结论是否仍然成立,不必证明;
(3)如图3,对旋转角α(60°<α<90°),猜想(1)中的结论是否仍然成立;若成立,请证明你的结论;若不成立,请说明理由.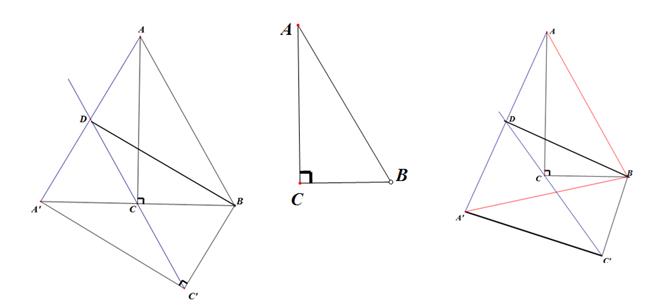
在平面直角坐标系 中,抛物线
中,抛物线 过点
过点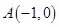 ,
,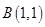 ,与
,与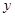 轴交于点
轴交于点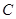 .
.
(1)求抛物线 的函数表达式;
的函数表达式;
(2)若点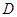 在抛物线
在抛物线 的对称轴上,当
的对称轴上,当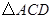 的周长最小时,求点
的周长最小时,求点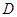 的坐标;
的坐标;
(3)在抛物线 的对称轴上是否存在点
的对称轴上是否存在点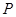 ,使
,使 成为以
成为以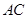 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点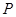 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
在四边形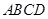 中,对角线
中,对角线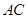 与
与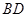 交于点
交于点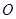 ,
,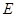 是
是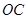 上任意一点,
上任意一点,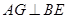 于点
于点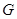 ,交
,交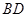 于点
于点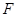 .
.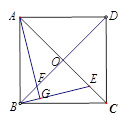

(1)如图1,若四边形 是正方形,判断
是正方形,判断 与
与 的数量关系;
的数量关系;
明明发现,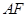 与
与 分别在
分别在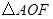 和
和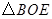 中,可以通过证明
中,可以通过证明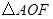 和
和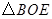 全等,得到
全等,得到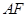 与
与 的数量关系;请回答:
的数量关系;请回答: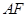 与
与 的数量关系是.
的数量关系是.
(2) 如图2,若四边形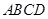 是菱形,
是菱形, 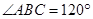 ,请参考明明思考问题的方法,求
,请参考明明思考问题的方法,求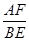 的值.
的值.