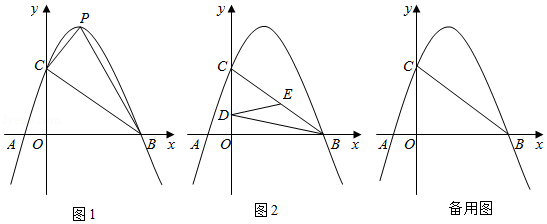
已知抛物线 与 轴交于 、 两点,与 轴交于 点,且点 的坐标为 、点 的坐标为 .
(1)求该抛物线的函数表达式;
(2)如图1,若该抛物线的顶点为 ,求 的面积;
(3)如图2,有两动点 、 在 的边上运动,速度均为每秒1个单位长度,它们分别从点 和点 同时出发,点 沿折线 按 方向向终点 运动,点 沿线段 按 方向向终点 运动,当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为 秒,请解答下列问题:
①当 为何值时, 的面积等于 ;
②在点 、 运动过程中,该抛物线上存在点 ,使得依次连接 、 、 、 得到的四边形 是平行四边形,请直接写出所有符合条件的点 的坐标.
(1)如图(1), 四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°,证明:BC+DC=AC.
(2) 如图(2),四边形ABCD中,AB=BC,∠ABC=60°,P为四边形ABCD内一点,且∠APD=120°,证明:PA+PD+PC≥BD
如图,已知在△ABC中,AB=AC,∠ABC>60°,∠ABD=60°,且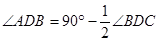 .求证:AB=BD+DC.
.求证:AB=BD+DC.
如图,已知△ABC中,AB=AC,∠A=100°,BD平分∠ABC,求证:BC=BD+AD.
如图,D是等边△ABC内一点,AD=BD,∠DBP=∠DBC,且BP=BA,求∠P的度数.
已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形.