如图,已知 是 的直径. 是 的弦,弦 垂直 于点 ,交 于点 .过点 作 的切线交 的延长线于点
(1)求证: ;
(2)判断 是否成立?若成立,请证明该结论;
(3)若 为 中点, , ,求 的长.

(25分)如图,在Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F,联结AD与内切圆相交于另一点P,联结PC、PE、PF.已知PC⊥PF.求证:
(1)EP/DE=PD/DC;(2)△EPD是等腰三角形.
实数x、y、z、w满足x≥y≥z≥w≥0,且5x+4y+3z+6w=100.求x+y+z+w的最大值和最小值.
如图,△ABC中, ,
, .点P在△ABC内,且
.点P在△ABC内,且 ,求△ABC的面积.
,求△ABC的面积.
如图,点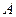 为
为 轴正半轴上一点,
轴正半轴上一点,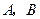 两点关于
两点关于 轴对称,过点
轴对称,过点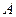 任作直线交抛物线
任作直线交抛物线 于
于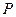 ,
, 两点
两点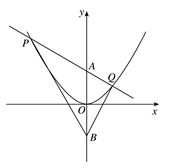
(1)求证:∠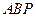 =∠
=∠ ;
;
(2)若点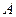 的坐标为(0,1),且∠
的坐标为(0,1),且∠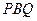 =60º,试求所有满足条件的直线
=60º,试求所有满足条件的直线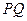 的函数解析式.
的函数解析式.
已知关于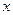 的一元二次方程
的一元二次方程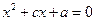 的两个整数根恰好比方程
的两个整数根恰好比方程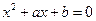 的两个根都大1,求
的两个根都大1,求 的值.
的值.