如图，点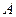
为
轴正半轴上一点，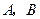
两点关于
轴对称，过点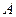任作直线交抛物线
于
，
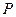两点
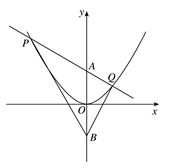
（1）求证：∠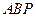
=∠
；
（2）若点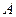的坐标为（0，1），且∠
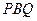=60º，试求所有满足条件的直线
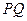的函数解析式.
如图，在等腰梯形ABCD中，AD＝4，BC＝9，∠B＝45°．动点P从点B出发沿BC向点C运动，动点Q同时以相同速度从点C出发沿CD向点D运动，其中一个动点到达端点时，另一个动点也随之停止运动．
（1）求AB的长；
（2）设BP＝x，问当x为何值时△PCQ的面积最大，并求出最大值；
（3）探究：在AB边上是否存在点M，使得四边形PCQM为菱形？请说明理由．
已知等腰梯形ABCD中，AD∥BC，∠B=45°，AD=2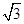
-2．动点P在折线BA-AD-DC上移动，若存在∠BPC=120°，且这样的P点恰好出现3次，求梯形ABCD的面积。
如图所示，在梯形ABCD中，AD∥BC，AB＝AD，∠BAD的平分线AE交BC于点E，连接DE．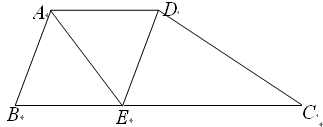
（1）求证：四边形ABED是菱形；
（2）若∠ABC＝60°，CE＝2BE，试判断△CDE的形状，并说明理由．
如图，在梯形ABCD中，AD∥BC，AD＝AB，过点A作AE∥DB交CB的延长线于点E．
（1）求证：∠ABD＝∠CBD；
（2）若∠C＝2∠E，求证：AB＝DC；
（3）在（2）的条件下，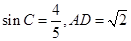
，求四边形AEBD的面积．
在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，AD=2，BC=BD=3，AC=4.
（1）求证:AC⊥BD
（2）求△AOB的面积