如图，直线y32x6与x轴交于点B，与y轴交于点A，点P为线-优题课

题文

如图，直线 $y = - \frac{3}{2} x + 6$ 与 $x$ 轴交于点 $B$ ，与 $y$ 轴交于点 $A$ ，点 $P$ 为线段 $AB$ 的中点，点 $Q$ 是线段 $OA$ 上一动点（不与点 $O$ 、 $A$ 重合）．

（1）请直接写出点 $A$ 、点 $B$ 、点 $P$ 的坐标；

（2）连接 $PQ$ ，在第一象限内将 $ΔOPQ$ 沿 $PQ$ 翻折得到 $ΔEPQ$ ，点 $O$ 的对应点为点 $E$ ．若 $∠ OQE = 90 °$ ，求线段 $AQ$ 的长；

（3）在（2）的条件下，设抛物线 $y = a x^{2} - 2 a^{2} x + a^{3} + a + 1 (a \neq 0)$ 的顶点为点 $C$ ．

①若点 $C$ 在 $ΔPQE$ 内部（不包括边），求 $a$ 的取值范围；

②在平面直角坐标系内是否存在点 $C$ ，使 $| CQ - CE |$ 最大？若存在，请直接写出点 $C$ 的坐标；若不存在，请说明理由．

科目数学题型解答题难度困难

知识点：二次函数的性质一次函数的性质一次函数图象与几何变换

登录免费查看答案和解析

相关试题

(6分)先化简，再求值．
(－)÷，其中x＝+1．

如图1，△ABC中，AB=AC=5cm，BC=6cm，边长为2cm的菱形DEFG两边DG、DE分别在AC、AB上．若菱形DEFG以1cm/s的速度沿射线AC方向平移．
（1）经过▲秒菱形DEFG的顶点F恰好在BC上；
（2）求菱形DEFG的面积；
（3）设菱形DEFG与△ABC的重合部分为Scm²，菱形DEFG平移的时间为t秒．求S与t的函数关系式．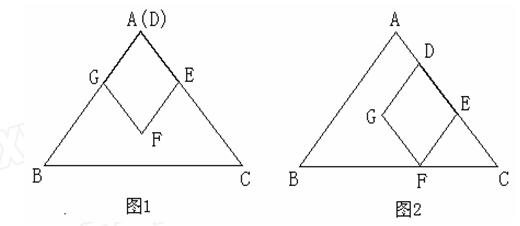

（8分）A、B两地相距630千米，客车、货车分别从A、B两地同时出发，匀速相向行驶．货车两小时可到达途中C站，客车需9小时到达C站（如图1所示）．货车的速度是客车的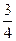，客、货车到C站的距离分别为y₁、y₂（千米），它们与行驶时间x（小
时）之间的函数关系如图2所示．

（1）求客、货两车的速度；
（2）求两小时后，货车到C站的距离y₂与行驶时间x之间的函数关系式；
（3）如图2，两函数图象交于点E，求E点坐标，并说明它所表示的实际意义．

我们通常可以对一些图形进行剪切,并利用图形的轴对称、平移、旋转等进行图案设计,如图1中,可以沿线段AE剪切矩形ABCD,再将△ABE通过变换与梯形
AECD拼接成等腰梯形.请按下列要求进行图案设计:
（1）把矩形剪切2次拼接成一个菱形，请在图2中画出剪切线，再画出拼接示意图；
（2）把矩形剪切１次拼接成一个菱形，请在图３中画出剪切线，再画出拼接示意图.

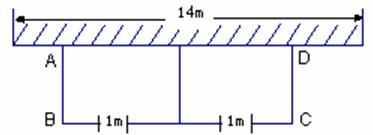
如图，要建一个面积为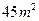的长方形养鸡场（分为两个区域），养鸡场的一边靠着一面长为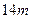的墙，另几条边用总长为的竹篱笆围成，每块区域的前面各开一个宽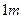的门．求这个养鸡场的长与宽．

试卷网试题网古诗词网作文网范文网