如图,抛物线 交 轴于 , 两点,交 轴于点 ,点 为线段 上的动点.
(1)求抛物线的解析式;
(2)求 的最小值;
(3)过点 作 交抛物线的第四象限部分于点 ,连接 , ,记 与 面积分别为 , ,设 ,求点 坐标,使得 最大,并求此最大值.

如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求证:四边形ABEF是菱形.
在一个口袋中有4个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸取一个小球然后放回,再随机地摸出一个小球,求下列事件的概率:
(1)两次取的小球的标号相同
(2)两次取的小球的标号的和等于4
已知二次函数 的图像过点(0,5).
的图像过点(0,5).
(1)求 的值,并写出这个二次函数的解析式.
的值,并写出这个二次函数的解析式.
(2)求出该二次函数图像的顶点坐标、对称轴.
已知关于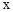 的一元二次方程
的一元二次方程 有两个相等的实数根.求
有两个相等的实数根.求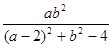 的值;
的值;
如果实数x满足 ,求代数式
,求代数式 的值
的值