等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题,在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.
(1)在直角三角形中,两直角边长分别为3和4,则该直角三角形斜边上的高的长为 ,其内切圆的半径长为 ;
(2)①如图1, 是边长为 的正 内任意一点,点 为 的中心,设点 到 各边距离分别为 , , ,连接 , , ,由等面积法,易知 ,可得 ;(结果用含 的式子表示)
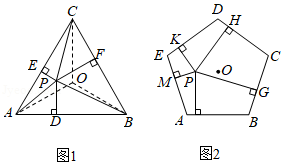
②如图2, 是边长为 的正五边形 内任意一点,设点 到五边形 各边距离分别为 , , , , ,参照①的探索过程,试用含 的式子表示 的值.(参考数据: ,
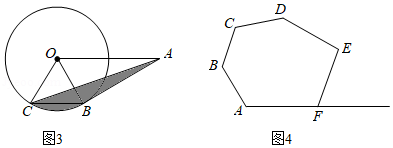
(3)①如图3,已知 的半径为2,点 为 外一点, , 切 于点 ,弦 ,连接 ,则图中阴影部分的面积为 ;(结果保留
②如图4,现有六边形花坛 ,由于修路等原因需将花坛进行改造,若要将花坛形状改造成五边形 ,其中点 在 的延长线上,且要保证改造前后花坛的面积不变,试确定点 的位置,并说明理由.
我国青海省玉树地区发生强烈地震以后,国家立即启动救灾预案,积极展开灾区运送救灾物资和对伤员的救治工作.已知西宁机场和玉树机场相距800千米,
乙两机沿同一航线各自从西宁、玉树出发,相向而行.如图,线段AB、CD分别表示甲、乙
两机离玉树机场的距离S(百千米)和所用去的时间t(小时)之间的函数关系的图象(注:
为了方便计算,将平面直角坐标系中距离S的单位定为(百千米)).观察图象回答下列问题:
(1)乙机在甲机出发后几小时,才从玉树机场出发?甲、乙两机的飞行速度每小时各为多少千米?
(2)求甲、乙两机各自的S与t的函数关系式;
(3)甲、乙两机相遇时,乙机飞行了几小时?离西宁机场多少千米?
如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,DE⊥AC,垂足为E.
(1)求证:点D是BC的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)如果⊙O的直径为9,cosB=,求DE的长.
如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)
如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.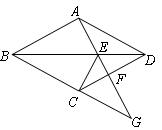
(1)求证:∠DAE=∠DCE;
(2)当AE=2EF时,判断FG与EF有何等量关系?并证明你的结论?
为了迎接扬州烟花三月经贸旅游节,某学校计划由七年级(1)班的3个小组(每个小组人数都相等)制作240面彩旗.后因一个小组另有任务,改由另外两个小组完成制作彩旗的任务,这样这两个小组的每一名学生就要比原计划多做4面彩旗.如果每名学生制作彩旗的面数相等,那么每个小组有多少学生?