已知抛物线 , , 是常数), .下列四个结论:
①若抛物线经过点 ,则 ;
②若 ,则方程 一定有根 ;
③抛物线与 轴一定有两个不同的公共点;
④点 , , , 在抛物线上,若 ,则当 时, .
其中正确的是 (填写序号).
阅读计算:(本题6分)
阅读下列各式: …
…
回答下列三个问题:
(1)验证: 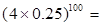 ;
;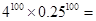 .
.
(2)通过上述验证, 归纳得出: ;
;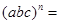 .
.
(3)请应用上述性质计算: 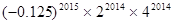
根据如图所示的计算程序,若输出的值y = 4,则输入的值x= .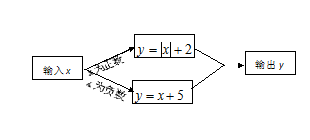
明明早晨去学校共用15分钟.他跑了一段,走了一段,他跑步的平均速度是250米/分钟,步行的平均速度是80米/分钟,他家离学校的距离是2900米,如果设他跑步的时间为x分钟,则列出的方程是 .
如果代数式 的值为3,那么代数式
的值为3,那么代数式 的值是 .
的值是 .
用火柴棒按以下方式搭“小鱼” .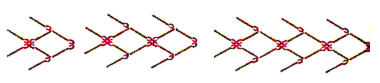
搭1条“小鱼”需用8根火柴棒,搭2条“小鱼”需用14根火柴棒,搭3条“小鱼”需用20根火柴棒……观察并找规律,搭10条“小鱼”需用火柴棒的根数为 .