小欣在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质.其研究过程如下:
(1)绘制函数图象
①列表:如表是 与 的几组对应值,其中 ;
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
②描点:根据表中的数值描点 ,请补充描出点 ;
③连线:用平滑的曲线顺次连接各点,请把图象补充完整.

(2)探究函数性质
判断下列说法是否正确(正确的填“ ”,错误的填“ ”
①函数值 随 的增大而减小: .
②函数图象关于原点对称: .
③ 函数图象与直线 没有交点: .
(1)已知角a和线段c如图所示,求作等腰三角形 ,使其底角∠B=a,腰长AB =" c," 要求仅用直尺和圆规作图,并保留作图痕迹. (不写作法)
,使其底角∠B=a,腰长AB =" c," 要求仅用直尺和圆规作图,并保留作图痕迹. (不写作法)
(2)若a=45O,c=2,求此三角形ABC的面积.
某服装厂生产一种西装和领带,西装每套定价600元,领带每条定价100元。厂方在开展促销活动期间,向客户提供两种优惠方案:
①西装和领带都按定价的90%付款;②买一套西装送一条领带。
现某客户要到该服装厂购买西装20套,领带 条(
条( )。
)。
(1)若该客户按方案①购买,需付款多少元?(用含 的代数式表示);
的代数式表示);
(2)若该客户按方案②购买,需付款多少元?(用含 的代数式表示)。
的代数式表示)。
(3)若 =30,通过计算说明此时按哪种方案购买较为合算?
=30,通过计算说明此时按哪种方案购买较为合算?
如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察下列问题。
(1)在第4个图中,共有白色瓷砖块;在第 个图中,共有白色瓷砖块;
个图中,共有白色瓷砖块;
(2)在第4个图中,共有瓷砖块;在第 个图中,共有瓷砖块;
个图中,共有瓷砖块;
(3)如果每块黑瓷砖4元,白瓷砖3元,铺设当 时,共需花多少钱购买瓷砖?
时,共需花多少钱购买瓷砖?
请你先认真阅读材料:
计算(-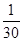 )÷(
)÷(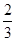 一
一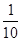 +
+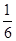 -
-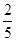 ).
).
解法l:解法2:
(-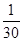 )÷(
)÷(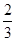 一
一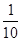 +
+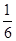 -
-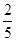 )原式的倒数为:
)原式的倒数为:
=(-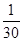 )÷[(
)÷[(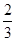 +
+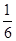 )-(
)-(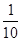 +
+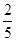 )](
)](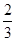 一
一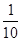 +
+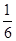 -
-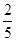 )÷(-
)÷(-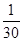 )
)
=(-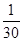 )÷(
)÷( -
-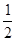 ) =(
) =(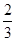 一
一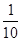 +
+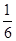 -
-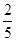 )×(-30)
)×(-30)
=(-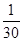 )÷
)÷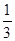 =-20+3-5+12
=-20+3-5+12
=-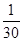 ×3 =(-20-5)+(3+12)
×3 =(-20-5)+(3+12)
=-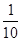 =-10
=-10
故原式=-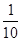
再根据你对所提供材料的理解,选择合适的方法计算:
(一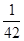 )÷(
)÷(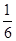 一
一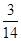 +
+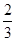 -
-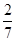 ).
).
请你做评委:在一堂数学活动课上,同在一合作学习小组的小明、小亮、小丁、小彭对刚学过的知识发表了自己的一些感受:
小明说:“绝对值不大于4的整数有7个。”
小丁说:“若 =3,
=3,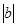 =2,则
=2,则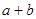 的值为5或1。”
的值为5或1。”
小亮说:“ <
< ,因为两个负数比较大小,绝对值大的数反而小。”
,因为两个负数比较大小,绝对值大的数反而小。”
小彭说:“多项式 是一次三项式。”
是一次三项式。”
依次判断四位同学的说法是否正确,如不正确,请帮他们修正,写出正确的说法。