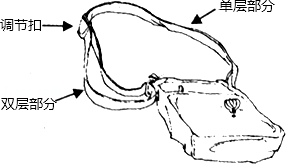
如图是一种单肩包，其背带由双层部分、单层部分和调节扣构成．小文购买时，售货员演示通过调节扣加长或缩短单层部分的长度，可以使背带的长度（单层部分与双层部分长度的和，其中调节扣所占长度忽略不计）加长或缩短，设双层部分的长度为 ，单层部分的长度为 ．经测量，得到表中数据．
双层部分长度 |
2 |
8 |
14 |
20 |
单层部分长度 |
148 |
136 |
124 |
112 |
（1）根据表中数据规律，求出 与 的函数关系式；
（2）按小文的身高和习惯，背带的长度调为 时为最佳背带长．请计算此时双层部分的长度；
（3）设背带长度为 ，求 的取值范围．
先化简再求值：
，其中
是一元二次方程
的根．
用适当的方法解下列方程
（1）
（2）
（3）
（4）
如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA＝3，OC＝2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．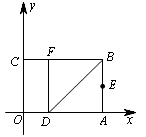
（1）直接写出点E、F的坐标；
（2）在y轴上是否存在点M，使得三角形MFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．
（3）设顶点为F的抛物线交y轴正半轴于点P，且以点E、F、P为顶点的三角形是等腰三角形，求该抛物线的解析式；若顶点为F的抛物线交y轴负半轴于点P，且以点E、F、P为顶点的三角形是等腰三角形， 请直接写出点P的坐标．
制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，设该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．
（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；
（2）根据工艺要求，当材料的温度低于20℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？
如图，以△ABC的边AB为直径作⊙O，交BC于D点，交AC于E点，BD=DE．
（1）求证：△ABC是等腰三角形
（2）若E是AC的中点，求弧BD的度数．