阅读下面的材料:
如果函数 满足:对于自变量 取值范围内的任意 , ,
(1)若 ,都有 ,则称 是增函数;
(2)若 ,都有 ,则称 是减函数.
例题:证明函数 是增函数.
证明:任取 ,且 , .
则 .
且 , ,
, .
,即 , .
函数 是增函数.
根据以上材料解答下列问题:
(1)函数 , (1) , (2) , (3) , (4) ;
(2)猜想 是 函数(填“增”或“减” ,并证明你的猜想.
如图,抛物线 与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N. 设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由)
(3)问:当x为何值时,△AGH是等腰三角形.
如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 3233 34 35 36
…………………………
(1)表中第8行的最后一个数是______________,它是自然数_____________的平方,第8行共有____________个数;
(2)用含n的代数式表示:第n行的第一个数是___________________,最后一个数是
________________,第n行共有_______________个数;
(3)求第n行各数之和.
如图,直角梯形纸片ABCD中,AD//BC,∠A=90º,∠C=30º.折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.
(1)求∠BDF的度数;
(2)求AB的长.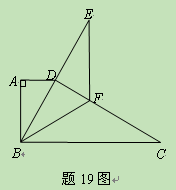
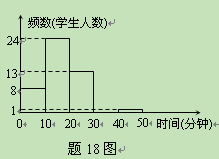
李老师为了解班里学生的作息时间表,调查了班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:
(1)此次调查的总体是什么?
(2)补全频数分布直方图;
(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比是多少?