如图,已知二次函数 的图象经过点 ,且与 轴交于原点及点 .
(1)求二次函数的表达式;
(2)求顶点 的坐标及直线 的表达式;
(3)判断 的形状,试说明理由;
(4)若点 为 上的动点,且 的半径为 ,一动点 从点 出发,以每秒2个单位长度的速度沿线段 匀速运动到点 ,再以每秒1个单位长度的速度沿线段 匀速运动到点 后停止运动,求点 的运动时间 的最小值.

如图,一次函数y=kx+b的图象与反比例函数y=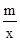 的图象交于
的图象交于
A(-2,1)B(1,n)两点.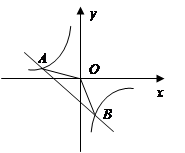
试确定上述反比例函数和一次函数的表达式
求△ABO的面积
根据图像直接写出当一次函数的值大于反比例函数的值时
x的取值范围。
阅读下列材料: ,
, ,
, ,……
,……
受此启发,请你解下面的方程: 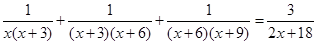
已知一次函数y=  图象过点A(0,3)B(2,4)题目中的矩形部分是一段因墨水污染而无法辨认的文字。
图象过点A(0,3)B(2,4)题目中的矩形部分是一段因墨水污染而无法辨认的文字。根据现有的信息,你能否求出题中的一次函数的解析式?若能,写出求解过程,若不能说明理由
根据关系式画出函数图象,
小明说“本题不用求函数关系式也能画出函数图象”,你认为对吗?为什么?
过点B能不能画出一直线BC将ABO(O为坐标原点)分成面积比为1:2的两部分?如能,可以画出几条,并写出这样的直线所对应的函数关系式,若不能,说明理由
如图,L ,L
,L 分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系。根据图像,回答下列问题:
分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系。根据图像,回答下列问题: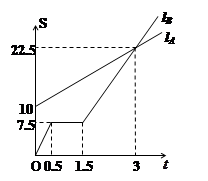
B出发时与A相距千米。
走了一段路后,自行车发生故障,进行修理,所用的时
间是小时。B出发后小时与A相遇
若B的自行车不发生故障,保持出发时的速度前进,那么与A的相遇点离B的出发点相距千米。在图中表示出这个相遇点C
如图所示,已知点A、E、F、D在同一条直线上,AE=DF,BF⊥AD,CE⊥AD, 垂足分别为F、E,BF=CE,求证:AB∥CD