如图所示，在平面直角坐标系xOy中，一次函数y2x的图象l与-优题课

题文

如图所示，在平面直角坐标系 $xOy$ 中，一次函数 $y = 2 x$ 的图象 $l$ 与函数 $y = \frac{k}{x} (k > 0, x > 0)$ 的图象（记为 $Γ)$ 交于点 $A$ ，过点 $A$ 作 $AB ⊥ y$ 轴于点 $B$ ，且 $AB = 1$ ，点 $C$ 在线段 $OB$ 上（不含端点），且 $OC = t$ ，过点 $C$ 作直线 $l_{1} / / x$ 轴，交 $l$ 于点 $D$ ，交图象 $Γ$ 于点 $E$ ．

（1）求 $k$ 的值，并且用含 $t$ 的式子表示点 $D$ 的横坐标；

（2）连接 $OE$ 、 $BE$ 、 $AE$ ，记 $ΔOBE$ 、 $ΔADE$ 的面积分别为 $S_{1}$ 、 $S_{2}$ ，设 $U = S_{1} - S_{2}$ ，求 $U$ 的最大值．

科目数学题型解答题难度较难

知识点：反比例函数与一次函数的交点问题二次函数的应用

登录免费查看答案和解析

相关试题

如图，在平面直角坐标系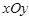中，二次函数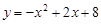的图象与一次函数的图象交于A、B两点，点A在x轴上，点B的纵坐标为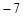．点P是二次函数图象上A、B两点之间的一个动点（不与点A、B重合），设点P的横坐标为m，过点P作x轴的垂线交AB于点C，作PD⊥AB于点D．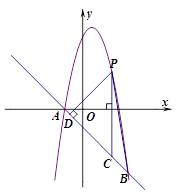

（1）求b及sin∠ACP的值；
（2）用含m的代数式表示线段PD的长；
（3）连接PB，线段PC把△PDB分成两个三角形，是否存在适合的m值，使这两个三角形的面积之比为．如果存在，直接写出m的值；如果不存在，请说明理由．

如图，正方形ABCD的对角线相交于点O，∠CAB的平分线分别交BD，BC于点E，F，作BH⊥AF于点H，分别交AC，CD于点G，P，连接GE，GF．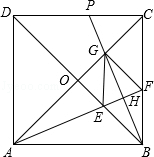

（1）求证：△OAE≌△OBG；
（2）试问：四边形BFGE是否为菱形？若是，请证明；若不是，请说明理由；
（3）试求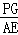：的值（结果保留根号）．

某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
（1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；
（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本=每件的成本×每天的销售量）

如图，一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子，继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°．求海底C点处距离海面DF的深度（结果精确到个位，参考数据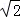：≈1．414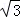，≈1．732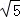，≈2．236）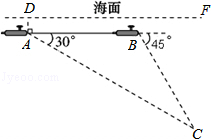

已知：如图，AB是⊙O的直径，AC是弦．过点A作∠BAC的角平分线，交⊙O于点D，过点D作AC的垂线，交AC的延长线于点E．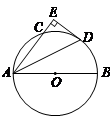

（1）求证：直线ED是⊙O的切线；
（2）连接EO，交AD于点F，若5AC=3AB，求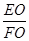的值．

试卷网试题网古诗词网作文网范文网