实践与探究
操作一:如图①,已知正方形纸片 ,将正方形纸片沿过点 的直线折叠,使点 落在正方形 的内部,点 的对应点为点 ,折痕为 ,再将纸片沿过点 的直线折叠,使 与 重合,折痕为 ,则 度.
操作二:如图②,将正方形纸片沿 继续折叠,点 的对应点为点 .我们发现,当点 的位置不同时,点 的位置也不同.当点 在 边的某一位置时,点 恰好落在折痕 上,则 度.
在图②中,运用以上操作所得结论,解答下列问题:
(1)设 与 的交点为点 .求证: ;
(2)若 ,则线段 的长为 .

(满分12分)如图,已知 是⊙O的直径,
是⊙O的直径, 是弦,过点
是弦,过点 作OD⊥AC于
作OD⊥AC于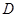 ,连结
,连结 .
.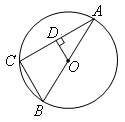
(1)求证:
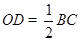 ;
;(2)若
 ,求∠
,求∠ 的度数.
的度数.
解分式方程:
(满分10分)阅读题例,解答下题:
例解方程
解:
(1)当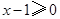 ,即
,即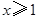 时(2)当
时(2)当 ,即
,即 时
时
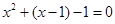


解得: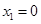 (不合题设,舍去),
(不合题设,舍去), 解得
解得 (不合题设,舍去)
(不合题设,舍去)
综上所述,原方程的解是
依照上例解法,解方程 .
.
先化简,再求值:


 +
+ ,其中x=2
,其中x=2 +1
+1解方程组

(本小题10分)某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现单价为60元时,年销售量可达5万件;若价格上涨,相应销量就会减少;当单价为80元时,销售量降至4万件,设销售单价为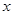 元.(
元.( 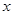 >60)
>60)①.用含x的代数式表示出年销售量;
②.当单价定为多少元时,年销售获利可达40万元?
③.当销售单价x为何值时,年获利最大?并求出这个最大值.