如图①,在 中, , , 是斜边 上的中线,点 为射线 上一点,将 沿 折叠,点 的对应点为点 .

(1)若 .直接写出 的长(用含 的代数式表示);
(2)若 ,垂足为 ,点 与点 在直线 的异侧,连接 ,如②,判断四边形 的形状,并说明理由;
(3)若 ,直接写出 的度数.
先化简,再求值: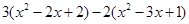 ,其中
,其中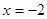 .
.
已知∠A和∠B互余,且∠A=40°30ˊ,求∠B的补角.
如图,线段AB=12cm,C是AB的中点.D是AC的中点,求DB.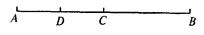
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.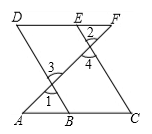
试说明:AC∥DF.
一辆汽车要将一批10cm厚的木板运往某建筑工地,进入工地到目的地前,遇有一段软地.聪明的司机协助搬运工将部分木板卸下铺在软地上,汽车顺利通过了.
(1)如果卸下部分木板后汽车对地面的压力为3000N,若设铺在软地上木板的面积为S㎡,汽车对地面产生的压强为P(N/㎡),那么P与S的函数关系式是.
(2)请在右侧直角坐标系中,作出相应的函数草图.
(3)若铺在软地上的木板面积是30㎡,则汽车对地面的压强是N/㎡.
(4)如果只要汽车对地面产生的压强不超过600N/㎡,汽车就能顺利通过,则铺在软地上的木板面积最少要㎡.