我市的前三岛是众多海钓人的梦想之地．小明的爸爸周末去前三岛钓-优题课

题文

我市的前三岛是众多海钓人的梦想之地．小明的爸爸周末去前三岛钓鱼，将鱼竿 $AB$ 摆成如图1所示．已知 $AB = 4.8 m$ ，鱼竿尾端 $A$ 离岸边 $0.4 m$ ，即 $AD = 0.4 m$ ．海面与地面 $AD$ 平行且相距 $1.2 m$ ，即 $DH = 1.2 m$ ．

（1）如图1，在无鱼上钩时，海面上方的鱼线 $BC$ 与海面 $HC$ 的夹角 $∠ BCH = 37 °$ ，海面下方的鱼线 $CO$ 与海面 $HC$ 垂直，鱼竿 $AB$ 与地面 $AD$ 的夹角 $∠ BAD = 22 °$ ．求点 $O$ 到岸边 $DH$ 的距离；

（2）如图2，在有鱼上钩时，鱼竿与地面的夹角 $∠ BAD = 53 °$ ，此时鱼线被拉直，鱼线 $BO = 5.46 m$ ，点 $O$ 恰好位于海面．求点 $O$ 到岸边 $DH$ 的距离．

（参考数据： $\sin 37 ° = \cos 53 ° \approx \frac{3}{5}$ ， $\cos 37 ° = \sin 53 ° \approx \frac{4}{5}$ ， $\tan 37 ° \approx \frac{3}{4}$ ， $\sin 22 ° \approx \frac{3}{8}$ ， $\cos 22 ° \approx \frac{15}{16}$ ， $\tan 22 ° \approx \frac{2}{5})$

科目数学题型解答题难度中等

知识点：解直角三角形的应用

登录免费查看答案和解析

相关试题

操作：小明准备制作棱长为1cm的正方体纸盒，现选用一些废弃的圆形纸片进行如下设计：

纸片利用率=×100%
发现：（1）方案一中的点A、B恰好为该圆一直径的两个端点．
你认为小明的这个发现是否正确，请说明理由．
（2）小明通过计算，发现方案一中纸片的利用率仅约为38.2%．
请帮忙计算方案二的利用率，并写出求解过程．
探究：（3）小明感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率．

“校园手机”现象越来越受到社会的关注．某校对本校若干名同学家长对“禁止中学生带手机到学校”现象的看法进行调查，根据调查的数据绘制成如下的条形统计图和扇形统计图．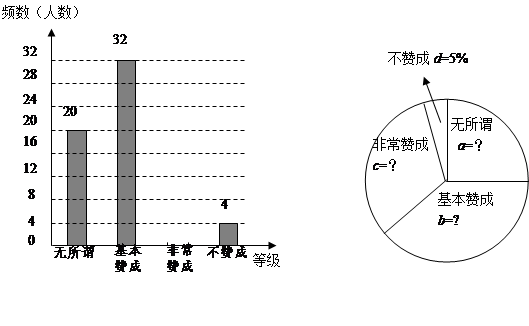

请根据以上不完整的统计图提供的信息，解答下列问题：
（1）该校共抽查了__________名同学的体育测试成绩，扇形统计图中A、B、C级所占的百分比分别为a=___________；b= ___________；c=_________；
（2）补全条形统计图；
（3）若该校同学共有1600名同学，请你估计该校同学家长认同孩子带手机有___________人．请你谈谈对这个调查结果的看法．

已知线段OA⊥OB，C为OB上中点，D为AO上一点，连AC、BD交于P点．

（1）如图1，当OA=OB且D为AO中点时，求的值；
（2）如图2，当OA=OB，=时，求△BPC与△ACO的面积之比．

已知，如图，在Rt△ABC中，∠C=90º，∠BAC的角平分线AD交BC边于D。
（1）以AB边上一点O为圆心，过A，D两点作⊙O（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由；
（2）若（1）中的⊙O与AB边的另一个交点为E，半径为2，AB=6,求线段AD、AE与劣弧DE所围成的图形面积．（结果保留根号和）

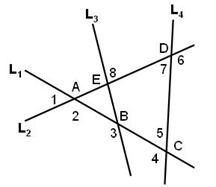
如图，有四条互相不平行的直线L₁、L₂、L₃、L₄所截出的八个角．请你任意选择其中的三个角（不可选择未标注的角），尝试找到它们的关系，并选择其中一组予以证明．

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号