为了提高广大职工对消防知识的学习热情，增强职工的消防意识，某单位工会决定组织消防知识竞赛活动，本次活动拟设一、二等奖若干名，并购买相应奖品．现有经费1275元用于购买奖品，且经费全部用完，已知一等奖奖品单价与二等奖奖品单价之比为 ．当用600元购买一等奖奖品时，共可购买一、二等奖奖品25件．
（1）求一、二等奖奖品的单价；
（2）若购买一等奖奖品的数量不少于4件且不超过10件，则共有哪几种购买方式？
利用角平分线的性质，找到△ABC内部距三边距离相等的点.
如右图，已知BE⊥AC于E，CF⊥AB于F，BE、CF相交于点D，若BD=CD.求证：AD平分∠BAC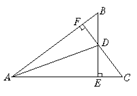
试用对称的观点分析说明线段的垂直平分线和角的平分线的联系与区别.
如图已知二次函数图象的顶点为原点，直线
的图象与该二次函数的图象交于A点(8，8)，直线与x轴的交点为C，与y轴的交点为B．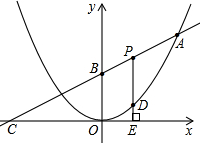
（1）求这个二次函数的解析式与B点坐标；
（2）P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于D点，与x轴交于点E．设线段PD的长为h，点P的横坐标为t，求h与t之间的函数关系式，并写出自变量t的取值范围；
（3）在（2）的条件下，在线段AB上是否存在点P，使得以点P、D、B为顶点的三角形与△BOC相似？若存在，请求出P点的坐标；若不存在，请说明理由．
如图，在△ABC中，已知AB=AC=5，BC=6，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE、始终经过点A，EF与AC交于M点．
（1）求证：△ABE∽△ECM；
（2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由．