如图,某地政府为解决当地农户网络销售农特产品物流不畅问题,计划打通一条东西方向的隧道 .无人机从点 的正上方点 ,沿正东方向以 的速度飞行 到达点 ,测得 的俯角为 ,然后以同样的速度沿正东方向又飞行 到达点 ,测得点 的俯角为 .
(1)求无人机的高度 (结果保留根号);
(2)求 的长度(结果精确到 .
(参考数据: , , ,

如图△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠GCA的平分线于点F.
(1)说明 EO=FO.
(2)当点O运动到何处,四边形AECF是矩形?说明你的结论.
(3)当点O运动到何处,AC与BC具有怎样的关系时,四边形AECF是正方形?为什么?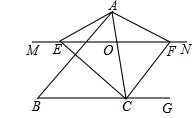
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O作直线EF⊥BD,分别交AD、BC于点E和点F,求证:四边形BEDF是菱形.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连结BF.
(1)线段BD与CD有何数量关系,为什么?
(2)当△ABC满足什么条件时,四边形AFBD是矩形?请说明理由.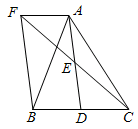
如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内.计算:∠PBA=∠PCQ=30°.
在△ABC中,AB=AC,点P为△ABC所在平面内一点.
(1)当点P在BC边上,过点P分别作PD∥AC交AB于点D,PE∥AB交AC于点E,如图1.证明:AB=PD+PE;
(2)当点P在△ABC外部时,过点P分别作PD∥AC交AB于点D,PE∥AB交AC于点E,交BC于点F,请你在图2中画出相应的图形,并直接写出PD,PE,PF与AB满足的数量关系.(不必说明理由)