如图,抛物线 交 轴于 , 两点,交 轴于点 ,动点 在抛物线的对称轴上.
(1)求抛物线的解析式;
(2)当以 , , 为顶点的三角形周长最小时,求点 的坐标及 的周长;
(3)若点 是平面直角坐标系内的任意一点,是否存在点 ,使得以 , , , 为顶点的四边形是菱形?若存在,请直接写出所有符合条件的点 的坐标;若不存在,请说明理由.

如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.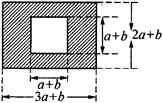
(1)(2x3y)3(-2xy)
(2)(a-2b)(a2-3ab+b2)
(3)(-3×105)·(7×104)·(-2×103)2
(4)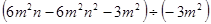
已知直线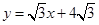 与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于C.
与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于C.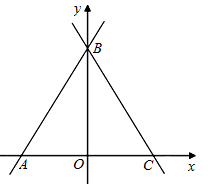
(1)求直线BC的解析式;
(2)若动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发沿C-B-A向点A运动(不与C、A重合),动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S,P点的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围;
(3)在(2)的条件下,当t=4秒时,y轴上有一点M,平面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由.
为丰富群众的业余生活,我市准备组织篮球比赛,市体育局策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)
方案二:直接购买门票方式如图所示.解答下列问题: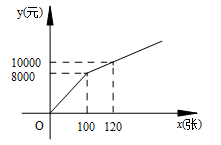
(1)方案一中,y与x的函数关系式为;
方案二中,当0≤x≤100时,y与x的函数关系式为,
当x>100时,y与x的函数关系式为;
(2)如果购买本场篮球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
如图,平行四边形 ABCD对角线交于点O,点E是线段BO上的动点(与点B、O不重合),连接CE,过A点作AF∥CE交BD于点F,连接AE与CF.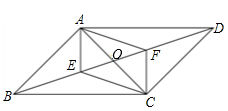
(1)求证:四边形AECF是平行四边形;
(2)当BA=BC=2,∠ABC=60°时,平行四边形 AECF能否成为正方形?若能,求出BE的长;若不能,请说明理由.