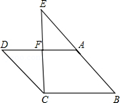
某工程队准备从 到 修建一条隧道,测量员在直线 的同一侧选定 , 两个观测点,如图.测得 长为 , 长为 , 长为 , , 、 、 、 在同一水平面内).
(1)求 、 两点之间的距离;
(2)求隧道 的长度.

如图,2012年4月10日,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?( ≈1.41,
≈1.41, ≈1.73,
≈1.73, =2.45).
=2.45).
某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练,物理、化学各有4各不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.
(1)请用树形图法或列表法,表示某个同学抽签的各种可能情况.
(2)小张同学对物理的①、②和化学的b、c号实验准备得较好,他同时抽到两科都准备的较好的实验题目的概率是多少?
如图,已知双曲线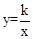 和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=
和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=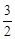 .
.
(1)求双曲线和和直线的解析式.
(2)求△AOB的面积.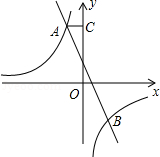
如图,四边形ABCD是平行四边形,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB,求证:△AEF≌△DFC.