二次函数 的图象经过点 , ,与 轴交于点 ,点 为第二象限内抛物线上一点,连接 、 ,交于点 ,过点 作 轴于点 .
(1)求二次函数的表达式;
(2)连接 ,当 时,求直线 的表达式;
(3)请判断: 是否有最大值,如有请求出有最大值时点 的坐标,如没有请说明理由.

(每题4分,共12分)用你喜欢的方法解下列方程:
(1)
(2)
(3)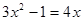
如图,在平面直角坐标系中,点A为二次函数y=-x2+4x-1图象的顶点,图象与y轴交于点C,过点A并与AC垂直的直线记为BD,点B,D分别为直线与y轴和x轴的交点,点E是二次函数图象上与点C关于对称轴对称的点,将一块三角板的直角顶点放在A点,绕点A旋转,三角板的两直角边分别与线段OD和线段OB相交于点P,Q两点.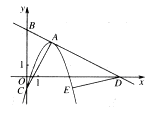
(1)点A的坐标为____,点c的坐标为____;
(2)求直线BD的表达式;
(3)在三角板旋转过程中,平面上是否存在点Q,使得以D,E,P,R为顶点的四边形为菱形?若存在,直接写出P,Q,R的坐标;若不存在,请说明理由.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=6,CD=AC=8,M、N分别是对角线BD、AC的中点.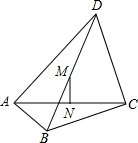
(1)求证:MN⊥AC.
(2)求MN的长.
对于平面直角坐标系中的任意两点A(a,b),B(c,d),我们把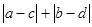 叫做A,B两点之间的直角距离,记作d(A,B).
叫做A,B两点之间的直角距离,记作d(A,B).
(1)已知O为坐标原点,
①若点P坐标为(-1,2),则d(O,P)=____;
②若Q(x,y)在第一象限,且满足d(O,Q)=2,请写出x与y之间满足的关系式,并在平面直角坐标系内画出符合条件的点Q组成的图形.
(2)设M是一定点,N是直线y=mx+n上的动点,我们把d(M,N)的最小值叫做M到直线y=mx+n的直角距离,试求点M(2,-l)到直线y=x+3的直角距离.
某五金店购进一批数量足够多的p型节能电灯 进价为35元/只,以50元/只销售,每天销售20只.市场调研发现:若每只每降l元,则每天销售数量比原来多3只.现商店决定对Q型节能电灯进行降价促销活动,每只降价x元(x为正整数).在促销期间,商店要想每天获得最大销售利润,每只应降价多少元?每天最大销售毛利润为多少?(注:每只节能灯的销售毛利润指每只节能灯的销售价与进货价的差)