某学校组织“一带一路”知识竞赛，有A，B两类问题，每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答，若回答错误则该同学比赛结束：若回答正确则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束.A类问题中的每个问题回答正确得20分，否则得0分：B类问题中的每个问题回答正确得80分，否则得0分，己知小明能正确回答A类问题的概率为0.8，能正确回答B类问题的概率为0.6，且能正确回答问题的概率与回答次序无关.
（1）若小明先回答A类问题，记 为小明的累计得分，求 的分布列；
（2）为使累计得分的期望最大，小明应选择先回答哪类问题？并说明理由.
如图02，在长方体ABCD－A1B1C1D1中，P、Q、R分别是棱AA1、BB1、BC上的点，PQ∥AB，C1Q⊥PR，求证：∠D1QR=90°．
点P在平面ABC的射影为O，且PA、PB、PC两两垂直，那么O是△ABC的( )
| A．内心 | B．外心 |
| C．垂心 | D．重心 |
在立体图形P－ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA＝AB，Q是PC中点．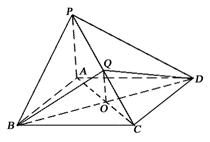
AC，BD交于O点．
（Ⅰ）求二面角Q－BD－C的大小：
（Ⅱ）求二面角B－QD－C的大小．
已知ABCD是边长为4的正方形，E、F分别是AB、AD的中点，GC垂直于ABCD所在的平面，且GC＝2．求点B到平面EFG的距离．
将矩形ABCD沿对角线BD折起来，使点C的新位置
在面ABC上的射影E恰在AB上．
求证：