记 是内角 , , 的对边分别为 , , .已知 ,点 在边 上, .
(1)证明: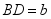 ;
;
(2)若
,求
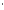
已知等差数列{an}的前n项的和记为Sn.如果a4=-12,a8=-4.
(1)求数列{an}的通项公式;(2)求Sn的最小值及其相应的n的值;
(3)从数列{an}中依次取出a1,a2,a4,a8,…, ,…,构成一个新的数列{bn},
,…,构成一个新的数列{bn},
求{bn}的前n项和
已知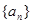 是等差数列,其前n项和为Sn,已知
是等差数列,其前n项和为Sn,已知
(1)求数列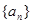 的通项公式;
的通项公式;
(2)设 ,证明
,证明 是等比数列,并求其前n项和Tn.
是等比数列,并求其前n项和Tn.
在 中,
中,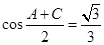 .
.
(1)求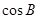 的值;(2)若
的值;(2)若 ,
, ,求
,求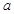 和
和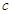 的值。
的值。
某同学利用暑假时间到一家商场勤工俭学,该商场向他提供了三种付款方式:第一种,每天支付38圆;第二种,第一天付4元,第二天付8元,第三天付12元,以此类推:第三种,第一天付0.4元,以后每天比前一天翻一番(即增加一倍),
你会选择哪种方式领取报酬呢?
设函数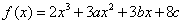 在
在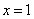 及
及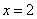 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的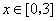 ,都有
,都有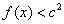 成立,求c的取值范围.
成立,求c的取值范围.