设函数 .
(1)求函数 的最小正周期;
(2)求函数 在 上的最大值.
在数列 中,a1=1,前
中,a1=1,前 项和为
项和为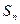 ,
,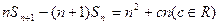 且
且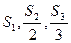 成等差数列。
成等差数列。
(1)求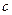 的值;(2)求数列
的值;(2)求数列 的通项公式。
的通项公式。
如图,在四棱锥 中,底面
中,底面 是边长为2的菱形,且
是边长为2的菱形,且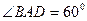 ,
, 为正三角形,
为正三角形,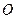 为
为 的中点,
的中点, 为棱
为棱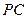 的中点
的中点
(1)求证: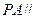 平面
平面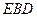
(2)求二面角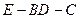 的大小
的大小
某电视台“挑战主持人”节目的挑战者闯第一关需要回答3个问题,其中前两个问
题回答正确各得10分,回答不正确各得0分,第三题回答正确得20分,回答不正确得-10分,总得分不少于30分即可过关.如果一位挑战者回答前两题正确的概率都是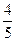 ,回答第三题正确的概率为
,回答第三题正确的概率为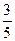 ,且各题回答正确与否相互之间没有影响.记这位挑战者回答这三个问题的总得分为
,且各题回答正确与否相互之间没有影响.记这位挑战者回答这三个问题的总得分为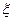 。
。
(1)求这位挑战者过关的概率有多大;(2)求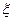 的概率分布和数学期望。
的概率分布和数学期望。
(本小题满分12分)设圆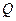 过点P(0,2), 且在
过点P(0,2), 且在 轴上截得的弦RG的长为4.(Ⅰ)求圆心
轴上截得的弦RG的长为4.(Ⅰ)求圆心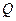 的轨迹E的方程;(Ⅱ)过点
的轨迹E的方程;(Ⅱ)过点 (0,1),作轨迹
(0,1),作轨迹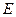 的两条互相垂直的弦
的两条互相垂直的弦 ,
, ,
,
设 、
、 的中点分别为
的中点分别为 ,
, ,试判断直线
,试判断直线 是否过定点?并说明理由.
是否过定点?并说明理由.
(本小题满分13分)一个袋中有大小相同的标有1,2,3,4,5,6的6个小球,某人做如下游戏,每次从袋中拿一个球(拿后放回),记下标号.若拿出球的标号是3的倍数,则得1分,否则得 分.
分.
(Ⅰ)求拿4次至少得2分的概率;(Ⅱ)求拿4次所得分数 的分布列和数学期望.
的分布列和数学期望.