阅读以下材料:
苏格兰数学家纳皮尔 . , 年)是对数的创始人.他发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉 , 年)才发现指数与对数之间的联系.
对数的定义:一般地,若 且 ,那么 叫做以 为底 的对数,记作 ,比如指数式 可以转化为对数式 ,对数式 可以转化为指数式 .
我们根据对数的定义可得到对数的一个性质:
, , , ,理由如下:
设 , ,则 , ,
,由对数的定义得 .
又 ,
.
根据上述材料,结合你所学的知识,解答下列问题:
(1)填空:① ,② ,③ ;
(2)求证: , , , ;
(3)拓展运用:计算 .
如图,已知⊙O的直径AB与弦CD相交于点E,AB⊥CD,⊙O的切线BF与弦AD的延长线相交于点F.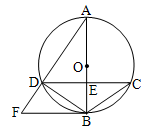
(1)求证:CD∥BF;
(2)若⊙O的半径为5,cos∠BCD=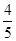 ,求线段AD与BF的长.
,求线段AD与BF的长.
如图,在马航失联客机“MH370”搜寻中需要确定疑似海面上油污带AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求油污带AB的长.(参考数据: =1.73)
=1.73)
已知二次函数y =" -"  x2 - x +
x2 - x + .
.
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当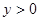 时,x的取值范围;
时,x的取值范围;
(3)若将此图象沿x轴向左平移1个单位,请写出平移后图象所对应的函数关系式.
甲、乙两个袋中均有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的数值分别为-7,-1,3,乙袋中的三张卡片上所标的数值分别为-2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用y表示取出的卡片上标的数值,把x、y分别作为点A的横坐标、纵坐标.
(1)用适当的方法写出点 的所有情况;
的所有情况;
(2)求点A落在第二象限的概率.
为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分)统计如下:
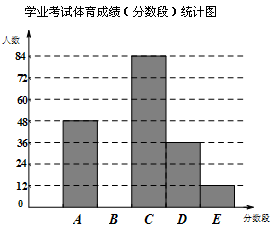
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为 ________,b的值为______,并将统计图补充完整;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数.”请问:甲同学的体育成绩应在什么分数段内?(填相应分数段的字母)
(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?