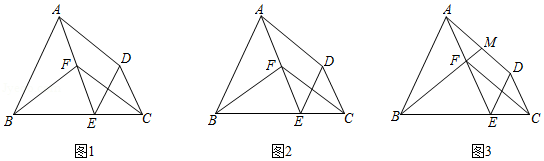
如图1,在四边形 中, ,点 在边 上,且 , ,作 交线段 于点 ,连接 .
(1)求证: ;
(2)如图2.若 , , ,求 的长;
(3)如图3,若 的延长线经过 的中点 ,求 的值.
已知⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(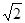 ,0),
,0), CAB="90°," AC=AB,顶点A在⊙O上运动.
CAB="90°," AC=AB,顶点A在⊙O上运动.
(1)设点A的横坐标为x,△ABC的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值;(2)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.
如图,在△ABC中,AB=AC,以AC为直径的半圆O交BC于点E,DE⊥AB,垂足为D.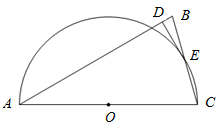
(1)求证:点E是BC的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)如果⊙O的直径为9,cosB= ,求DE的长.
,求DE的长.
在平面直角坐标系xOy中,二次函数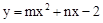 的图象过A(-1,-2)、B(1,0)两点.
的图象过A(-1,-2)、B(1,0)两点.
(1)求此二次函数的解析式并画出二次函数图象;
(2)点P(t,0)是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
一学校为了绿化校园环境,向某园林公司购买力一批树苗,园林公司规定:如果购买树苗不超过60棵,每棵售价120元;如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗最低售价不得少于100元,该校最终向园林公司支付树苗款8800元,请问该校共购买了多少棵树苗?
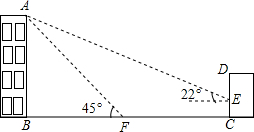
如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22º时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45º时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).求教学楼AB的高度.(参考数据:sin22º≈ ,cos22º≈
,cos22º≈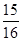 ,tan22º≈
,tan22º≈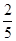 )
)