为了弘扬爱国主义精神，某校组织了"共和国成就"知识竞赛，将成绩分为： （优秀）、 （良好）、 （合格）、 （不合格）四个等级．小李随机调查了部分同学的竞赛成绩，绘制了如图统计图．
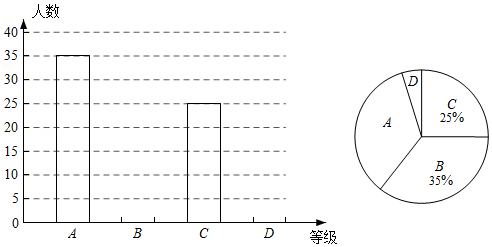
（1）本次抽样调查的样本容量是 ，请补全条形统计图；
（2）已知调查对象中只有两位女生竞赛成绩不合格，小李准备随机回访两位竞赛成绩不合格的同学，请用树状图或列表法求出恰好回访到一男一女的概率；
（3）该校共有2000名学生，请你估计该校竞赛成绩"优秀"的学生人数．
(1)
(2)
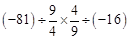
（3）
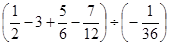
（4）
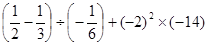
(5) 
(6)
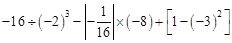
如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90°，点E是DC的中点，过点E作DC的垂线交AB于点P，交CB的延长线于点M．点F在线段ME上，且满足CF＝AD，MF＝MA．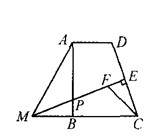
(1)若∠MFC＝120°，求证：AM＝2MB；
(2)求证：∠MPB＝90°－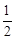
∠FCM．
若△ABC的三边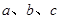
满足条件:a2＋b2＋c2＋338＝10a＋24b＋26c，试判断△ABC的形状．
如图，在梯形ABCD中，AD∥BC，AB＝DC＝AD，BC＝AC，求该梯形各内角的度数．
如图，△ABC中，AD是∠BAC的平分线，DE⊥AB，DF⊥AC， E、F为垂足，连接EF交AD于G，试判断AD与EF垂直吗？并说明理由. 