根据数学家凯勒的"百米赛跑数学模型",前30米称为"加速期",30米 米为"中途期",80米 米为"冲刺期".市田径队把运动员小斌某次百米跑训练时速度 与路程 之间的观测数据,绘制成曲线如图所示.
(1) 是关于 的函数吗?为什么?
(2)"加速期"结束时,小斌的速度为多少?
(3)根据如图提供的信息,给小斌提一条训练建议.

李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.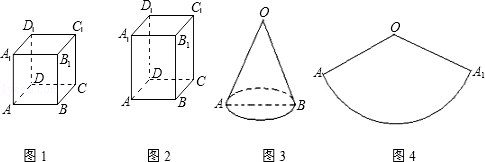
(1)如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;
(2)如图2,正四棱柱的底面边长为5cm,侧棱长为6cm,一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处;
(3)如图3,圆锥的母线长为4cm,圆锥的侧面展开图如图4所示,且∠AOA1=120°,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.
(1)设a、b、c、d为正实数,a<b,c<d,bc>ad,有一个三角形的三边长分别为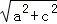 ,
,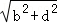 ,
,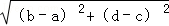 ,求此三角形的面积;
,求此三角形的面积;
(2)已知a,b均为正数,且a+b=2,求U=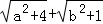 的最小值.
的最小值.
(1)化简:
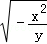 •(﹣4
•(﹣4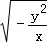 )÷
)÷
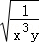
(2)已知x= ﹣1,求x2+3x﹣1的值.
﹣1,求x2+3x﹣1的值.
如图,在△ABC中,AB= +1,AC=
+1,AC= ,BC=2,求△ABC三个内角的度数.
,BC=2,求△ABC三个内角的度数.
已知x=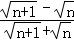 ,y=
,y= ,且19x2+123xy+19y2=1985.试求正整数n.
,且19x2+123xy+19y2=1985.试求正整数n.