在直角梯形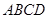 中,
中,  , 高
, 高 (如图1). 动点
(如图1). 动点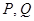 同时从点
同时从点 出发, 点
出发, 点 沿
沿 运动到点
运动到点 停止, 点
停止, 点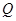 沿
沿 运动到点
运动到点 停止,两点运动时的速度都是1cm/s,而当点
停止,两点运动时的速度都是1cm/s,而当点 到达点
到达点 时,点
时,点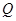 正好到达点
正好到达点 . 设
. 设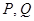 同时从点
同时从点 出发,经过的时间为
出发,经过的时间为 (s)时,
(s)时,  的面积为
的面积为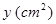 (如图2). 分别以
(如图2). 分别以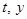 为横、纵坐标建立直角坐标系, 已知点
为横、纵坐标建立直角坐标系, 已知点 在
在 边上从
边上从 到
到 运动时,
运动时, 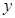 与
与 的函数图象是图3中的线段
的函数图象是图3中的线段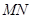 .
.
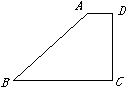

(图1) (图2) (图3)
(1)分别求出梯形中 的长度;
的长度;
(2)分别写出点 在
在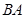 边上和
边上和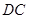 边上运动时,
边上运动时, 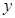 与
与 的函数关系式(注明自变量的取值范围), 并在图3中补全整个运动中
的函数关系式(注明自变量的取值范围), 并在图3中补全整个运动中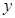 关于
关于 的函数关系的大致图象.
的函数关系的大致图象.
(3)问:是否存在这样的t,使PQ将梯形ABCD的面积恰好分成1:6的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
先化简再求值: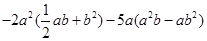 , 其中
, 其中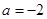 ,
,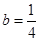 .
.
计算(每小题3分,共12分)
(1) ;
;
(2) ;
;
(3) ;
;
(4) .
.
(本题4分)(1)如图,点M是△ABC中AB的中点,经平移后,点M落在M’处.请在正方形网格中画出△ABC平移后的图形△A’B’C’.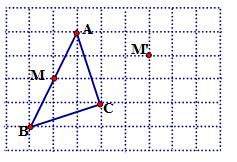
(2)若图中一小网格的边长为1,则△ABC的面积为_____.
如图1,已知直线y=2x+2与y轴、x轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC
(1)求点C的坐标,并求出直线AC的关系式.
(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.
(3)如图3,在(1)的条件下,直线AC交x轴于M,P(−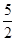 ,k)是线段BC上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
,k)是线段BC上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.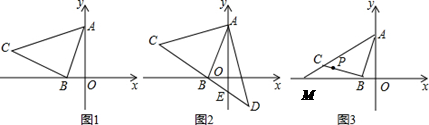
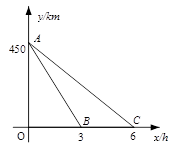
一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速
运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示.慢车离甲地的路
程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段AC所示.根据图像进行以下研究.
解读信息:(1)甲、乙两地之间的距离为km;
(2)线段AB的解析式为;两车在慢车出发小时后相遇;
问题解决:
(3)设快、慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数的图像.