探究函数性质时,我们经历了列表、描点、连线画函数图象,观察分析图象特征,概括函数性质的过程.以下是我们研究函数 性质及其应用的部分过程,请按要求完成下列各小题.
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
6 |
5 |
4 |
|
2 |
1 |
|
7 |
|
(1)写出函数关系式中 及表格中 , 的值:
, , ;
(2)根据表格中的数据在所给的平面直角坐标系中画出该函数的图象,并根据图象写出该函数的一条性质: ;
(3)已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.

甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 ,桥拱顶点 到水面的距离是 .
(1)按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;
(2)一只宽为 的打捞船径直向桥驶来,当船驶到桥拱下方且距 点 时,桥下水位刚好在 处,有一名身高 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平).
(3)如图③,桥拱所在的函数图象是抛物线 ,该抛物线在 轴下方部分与桥拱 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 个单位长度,平移后的函数图象在 时, 的值随 值的增大而减小,结合函数图象,求 的取值范围.

如图,在 中, 为 的直径, 为 的弦,点 是 的中点,过点 作 的垂线,交 于点 ,交 于点 ,分别连接 , .
(1) 与 的数量关系是 ;
(2)求证: ;
(3)若 , ,求阴影部分图形的面积.

为庆祝"中国共产党的百年华诞",某校请广告公司为其制作"童心向党"文艺活动的展板、宣传册和横幅,其中制作宣传册的数量是展板数量的5倍,广告公司制作每件产品所需时间和利润如表:
|
产品 |
展板 |
宣传册 |
横幅 |
|
制作一件产品所需时间(小时) |
1 |
|
|
|
制作一件产品所获利润(元 |
20 |
3 |
10 |
(1)若制作三种产品共计需要25小时,所获利润为450元,求制作展板、宣传册和横幅的数量;
(2)若广告公司所获利润为700元,且三种产品均有制作,求制作三种产品总量的最小值.
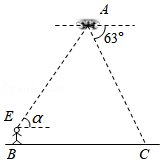
随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量广场 , 两点之间的距离.如图所示,小星站在广场的 处遥控无人机,无人机在 处距离地面的飞行高度是 ,此时从无人机测得广场 处的俯角为 ,他抬头仰视无人机时,仰角为 ,若小星的身高 , (点 , , , 在同一平面内).
(1)求仰角 的正弦值;
(2)求 , 两点之间的距离(结果精确到 .
, , , , ,
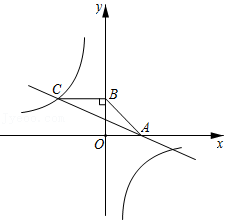
如图,一次函数 的图象与反比例函数 的图象交于点 ,与 轴交于点 ,过点 作 轴,垂足为 ,若 .
(1)求点 的坐标及 的值;
(2)若 ,求一次函数的表达式.