某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次 空气质量等级 |
[0,200] |
(200,400] |
(400,600] |
1(优) |
2 |
16 |
25 |
2(良) |
5 |
10 |
12 |
3(轻度污染) |
6 |
7 |
8 |
4(中度污染) |
7 |
2 |
0 |
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天"空气质量好";若某天的空气质量等级为3或4,则称这天"空气质量不好".根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
人次≤400 |
人次>400 |
|
空气质量好 |
||
空气质量不好 |
附: ,
P( K 2≥ k) |
0.050 |
0.010 |
0.001 |
k |
3 |
6.635 |
10.828 |
若函数y=f(x)是周期为2的偶函数,当x∈[2,3]时,f(x)=x-1.在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中2<a<3),
(1)求当x∈[1,2]时,f(x)的解析式;
(2)定点C的坐标为(0,a)(其中2<a<3),求△ABC面积的最大值.
已知函数 ,若存在
,若存在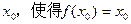 ,则
,则
称是函数 的一个不动点,设
的一个不动点,设
(Ⅰ)求函数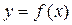 的不动点;
的不动点;
(Ⅱ)对(Ⅰ)中的二个不动点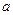 、
、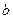 (假设
(假设 ),求使
),求使
恒成立的常数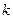 的值;
的值;
已知函数y=f(x)= (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .试求函数f(x)的解析式
.试求函数f(x)的解析式
已知集合A={x| x2-3x-10≤0},B={x| m+1≤x≤2m-1},若A B且B≠
B且B≠ ,求实数m的取值范围。
,求实数m的取值范围。
设全集 ,集合
,集合 ,集合
,集合
(Ⅰ)求集合 与
与 ; (Ⅱ)求
; (Ⅱ)求 、
、