若函数y=f(x)是周期为2的偶函数,当x∈[2,3]时,f(x)=x-1.在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中2<a<3),
(1)求当x∈[1,2]时,f(x)的解析式;
(2)定点C的坐标为(0,a)(其中2<a<3),求△ABC面积的最大值.
如图甲,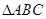 是边长为6的等边三角形,
是边长为6的等边三角形,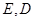 分别为
分别为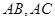 靠近
靠近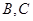 的三等分点,点
的三等分点,点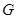 为边
为边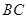 边的中点,线段
边的中点,线段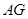 交线段
交线段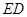 于点
于点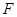 .将
.将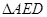 沿
沿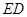 翻折,使平面
翻折,使平面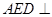 平面
平面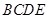 ,连接
,连接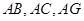 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.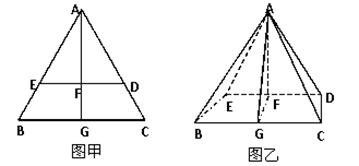
(1)求证: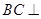 平面
平面
(2)求四棱锥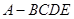 的体积.
的体积.
某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校,求抽取的2所学校均为小学的概率.
已知向量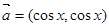 ,
,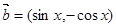 ,设函数
,设函数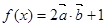 .
.
(1)求函数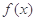 的最小正周期;
的最小正周期;
(2)求函数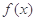 在区间
在区间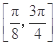 上的最小值和最大值.
上的最小值和最大值.
已知公比不为1的等比数列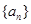 的前
的前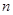 项和为
项和为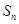 ,
,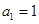 ,且
,且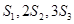 成等差数列.
成等差数列.
(1)求数列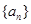 的通项公式;
的通项公式;
(2)设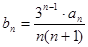 ,求数列
,求数列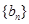 的前
的前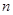 项和
项和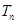 .
.
已知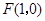 ,直线
,直线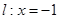 ,
,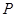 为平面上的动点,过点
为平面上的动点,过点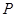 作
作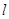 的垂线,垂足为点
的垂线,垂足为点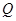 ,且
,且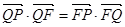 .
.
(1)求动点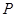 的轨迹曲线
的轨迹曲线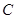 的方程;
的方程;
(2)设动直线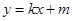 与曲线
与曲线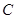 相切于点
相切于点 ,且与直线
,且与直线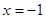 相交于点
相交于点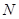 ,试探究:在坐标平面内是否存在一个定点
,试探究:在坐标平面内是否存在一个定点 ,使得以
,使得以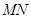 为直径的圆恒过此定点
为直径的圆恒过此定点 ?若存在,求出定点
?若存在,求出定点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.