某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得 , , , , .
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=
,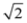 ≈1.414.
≈1.414.
(本小题满分12分)关于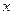 的不等式
的不等式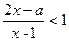 的解集为P, 不等式
的解集为P, 不等式 的解集为Q,若P
的解集为Q,若P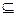 Q,求实数
Q,求实数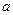 的取值范围。
的取值范围。
若定义在R上的函数 对任意的
对任意的 ,都有
,都有 成立,且当
成立,且当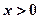 时,
时,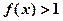 。
。
(1)求证: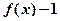 为奇函数;
为奇函数;
(2)求证: 是R上的增函数;
是R上的增函数;
(3)设集合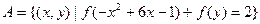 ,
, ,且
,且 , 求实数
, 求实数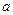 的取值范围。
的取值范围。
(本题12分)若二次函数满足 。
。
(1) 求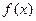 的解析式;
的解析式;
(2) 若在区间[-1,1]上不等式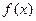 >2x+m恒成立,求实数m的取值范围。
>2x+m恒成立,求实数m的取值范围。
已知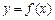 是定义在R上的函数,对于任意的
是定义在R上的函数,对于任意的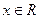 ,
, ,且当
,且当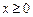 时,
时,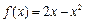 .
.
(1)求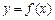 的解析式;
的解析式;
(2)画出函数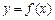 的图象,并指出
的图象,并指出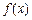 的单调区间及在每个区间上的增减性;
的单调区间及在每个区间上的增减性;
(3)若函数f(x)在区间[-1,a-2]上单调递增,试确定a的取值范围.
函数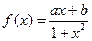 是定义在
是定义在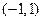 上的奇函数,且
上的奇函数,且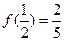 ,
,
(1)确定函数 的解析式;
的解析式;
(2)判断 在
在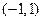 上的单调性并用定义证明.
上的单调性并用定义证明.
(3)解不等式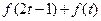 <0;
<0;