(本小题满分12分)如图,椭圆的右焦点 与抛物线
与抛物线 的焦点重合,过
的焦点重合,过 且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且
且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且

(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P为椭圆上一点,若过点M(2,0)的直线 与椭圆相交于不同两点A和B,且满足
与椭圆相交于不同两点A和B,且满足 (O为坐标原点),求实数t的取值范围.
(O为坐标原点),求实数t的取值范围.
(本小题满分12分)
在平面直角坐标系中, 为原点,
为原点,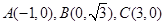 ,动点
,动点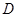 满足
满足 ,求(Ⅰ)动点
,求(Ⅰ)动点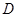 的轨迹;(Ⅱ)求
的轨迹;(Ⅱ)求 的最大值.
的最大值.
(本小题满分12分)
设 的内角A、B、C的对边长分别为a、b、c,且3
的内角A、B、C的对边长分别为a、b、c,且3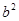 +3
+3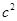 -3
-3 =4
=4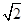 bc .
bc .
(Ⅰ) 求 的值;
的值;
(Ⅱ)求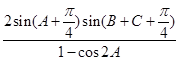 的值.
的值.
若某产品的直径长与标准值的差的绝对值不超过 时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:
时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位: )将所得数据分组,得到如下频率分布表:
)将所得数据分组,得到如下频率分布表:
(1)将上面表格中缺少的数据填充完整;
(2)估计该厂生产的此种产品中,不合格的直径长与标准值的差落在区间 内的概率
内的概率
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品,据此估算这批产品中的合格品的件数.
某河流上的一座水力发电站,每年六月份的发电量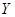 (单位:万千瓦时)与该河上游在六月份的降雨量
(单位:万千瓦时)与该河上游在六月份的降雨量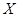 (单位:毫米)有关据统计,当
(单位:毫米)有关据统计,当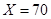 时,
时, ;
;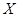 每增加10,
每增加10,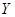 增加5.已知近20年
增加5.已知近20年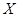 的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(1)完成如下的频率分布表:近20年六月份降雨量频率分布表
(2)假定今年六月份的降雨量与近20年六月份降雨量的分布规律相同,并将频率视为概率,求今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(Ⅰ)求应从小学、中学、大学中分别抽取的学校数目;
(Ⅱ)若从抽取的6所学校中随机抽取2所学校做进一步数据分析.
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率.