已知椭圆C1: (a>b>0)的右焦点F与抛物线C2的焦点重合,C1的中心与C2的顶点重合.过F且与x轴重直的直线交C1于A,B两点,交C2于C,D两点,且|CD|= |AB|.
(1)求C1的离心率;
(2)若C1的四个顶点到C2的准线距离之和为12,求C1与C2的标准方程.
.(本小题满分12分)
某种产品的广告费支出 与销售额
与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
(Ⅰ)求回归直线方程;
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(Ⅲ)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对
值不超过5的概率。(参考数据:

 )
)
(本小题满分12分)等差数列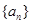 中,已知
中,已知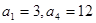 ,
,
(I)求数列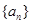 的通项公式;
的通项公式;
(Ⅱ)若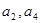 分别为等比数列
分别为等比数列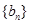 的第1项和第2项,试求数列
的第1项和第2项,试求数列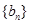 的通项公式及前
的通项公式及前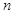
项和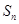 .
.
(本小题满分12分)如图,四边形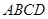 与
与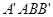 都是边长为
都是边长为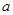 的正方形,点E是
的正方形,点E是 的中点,
的中点,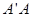 ⊥平面ABCD.
⊥平面ABCD.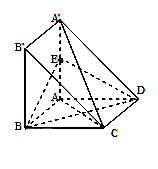
(I)计算:多面体A'B'BAC的体积;
(II)求证: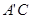
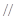 平面BDE;
平面BDE;
(Ⅲ) 求证:平面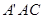 ⊥平面BDE.
⊥平面BDE.
(本小题满分12分)
设平顶向量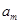 = ( m , 1),
= ( m , 1), 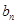 =" (" 2 , n ),其中 m, n
=" (" 2 , n ),其中 m, n 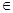 {1,2,3,4}.
{1,2,3,4}.
(I)请列出有序数组( m,n )的所有可能结果;
(II)记“使得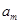
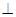 (
(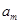 -
-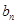 )成立的( m,n )”为事件A,求事件A发生的概率。
)成立的( m,n )”为事件A,求事件A发生的概率。
设A(x1,y1)、B(x2,y2)是函数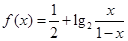 的图象上任两点,且
的图象上任两点,且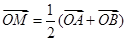 ,已知点M横坐标为
,已知点M横坐标为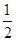 ,
,
(1)求点M的纵坐标;
(2)若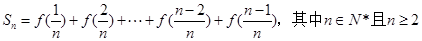 ,求Sn。
,求Sn。
(3)已知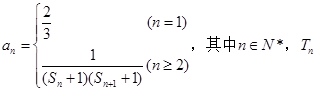 为数列{an}的前n项和, 若
为数列{an}的前n项和, 若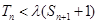 对一切
对一切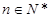 都成立,求
都成立,求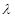 取值范围。
取值范围。