某校为举办甲、乙两项不同活动，分别设计了相应的活动方案：方案一、方案二．为了解该校学生对活动方案是否支持，对学生进行简单随机抽样，获得数据如下表：
男生 |
女生 |
|||
支持 |
不支持 |
支持 |
不支持 |
|
方案一 |
200人 |
400人 |
300人 |
100人 |
方案二 |
350人 |
250人 |
150人 |
250人 |
假设所有学生对活动方案是否支持相互独立．
（Ⅰ）分别估计该校男生支持方案一的概率、该校女生支持方案一的概率；
（Ⅱ）从该校全体男生中随机抽取2人，全体女生中随机抽取1人，估计这3人中恰有2人支持方案一的概率；
（Ⅲ）将该校学生支持方案的概率估计值记为 ，假设该校年级有500名男生和300名女生，除一年级外其他年级学生支持方案二的概率估计值记为 ，试比较 与 的大小．（结论不要求证明）
在直角坐标系xOy中，椭圆C的参数方程为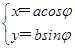
(φ为参数，a>b>0)，在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴)中，直线l与圆O的极坐标方程分别为ρsin(θ＋
)＝
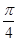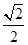m(m为非零数)与ρ＝b.若直线l经过椭圆C的焦点，且与圆O相切，求椭圆C的离心率．
已知曲线C1的参数方程是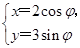
(φ为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ＝2.正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为
.
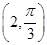(1)求点A，B，C，D的直角坐标；
(2)设P为C1上任意一点，求|PA|2＋|PB|2＋|PC|2＋|PD|2的取值范围．
已知曲线C1的参数方程为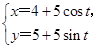
(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝2sin θ.
(1)把C1的参数方程化为极坐标方程；
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)．
已知矩阵M＝
有特征值λ1＝4及对应的一个特征向量e1＝
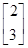.求：
(1)矩阵M；
(2)曲线5x2＋8xy＋4y2＝1在M的作用下的新曲线方程．
已知矩阵M＝
，△ABC的顶点为A(0,0)，B(2,0)，C(1,2)，求△ABC在矩阵M－1的变换作用下所得△A′B′C′的面积．